题目内容

设椭圆的参数方程为
x=acosθ
y=bsinθ
(0≤θ≤π)，M（x1，y1），N（x2，y2）是椭圆上两点，M，N对应的参数为θ1，θ2且x1＜x2，则（　　）
分析：利用椭圆的参数方程，可得cosθ1＜cosθ2，借助于余弦函数的单调性，即可得结论．
解答：解：由题意，M（x1，y1），N（x2，y2）是椭圆上两点，M，N对应的参数为θ1，θ2且x1＜x2，
∴acosθ1＜acosθ2
∴cosθ1＜cosθ2
∵0≤θ1≤π，0≤θ2≤π
∴θ1＞θ2
故选B．
点评：本题的考点是椭圆的参数方程，考查余弦函数的单调性，属于基础题．
练习册系列答案
相关题目
精英家教网附加题：
A．如图，四边形ABCD内接于圆O，弧AB=弧AD，过A点的切线交CB的延长线于E点．
求证：AB2=BE•CD．
B．设数列{an}，{bn}满足an+1=3an+2bn，bn+1=2bn，且满足
an+4
bn+4
=M
an
bn
，试求二阶矩阵M．
C．已知椭圆C的极坐标方程为ρ2=
12
3cos2θ+4sin2θ
，点F1，F2为其左、右焦点，直线l的参数方程为
x=2+
2
2
t
y=
2
2
t
（t为参数，t∈R）．求点F1，F2到直线l的距离之和．
D．已知x，y，z均为正数．求证：
x
yz
+
y
zx
+
z
xy
≥
1
x
+
1
y
+
1
z
．
设x=3 cosφ,φ为参数，椭圆=1的参数方程为____________________.

本题有（1）、（2）、（3）三个选考题，每题7份，请考生任选2题作答，满分14分.

如果多做，则按所做的前两题计分.

选修4系列（本小题满分14分）

   （1）（本小题满分7分）选修4-2：矩阵与变换

设是把坐标平面上的点的横坐标伸长到倍，纵坐标伸长到倍的伸压变换．

（Ⅰ）求矩阵的特征值及相应的特征向量；

（Ⅱ）求逆矩阵以及椭圆在的作用下的新曲线的方程．

(2) （本小题满分7分）选修4-4：坐标系与参数方程

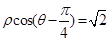直角坐标系中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，已知直线l的极坐标方程，曲线C的参数方程为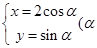为参数），求曲线C截直线l所得的弦长

（3）（本小题满分7分）选修4—5：不等式选讲

已知，且、、是正数，求证：.

 
附加题：
A．如图，四边形ABCD内接于圆O，弧AB=弧AD，过A点的切线交CB的延长线于E点．
求证：AB2=BE•CD．
B．设数列{an}，{bn}满足an+1=3an+2bn，bn+1=2bn，且满足=M，试求二阶矩阵M．
C．已知椭圆C的极坐标方程为，点F1，F2为其左、右焦点，直线l的参数方程为（t为参数，t∈R）．求点F1，F2到直线l的距离之和．
D．已知x，y，z均为正数．求证：．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网