Question

【题目】已知是定义域为的奇函数,当时, .

(1)写出函数的解析式.

(2)若方程恰有3个不同的解,求的取值范围.

Answer 1

【答案】（1）f(x)= ；（2）.

【解析】试题分析：（1）设，则，结合的解析式及的定义域为的奇函数即可求得函数的解析式；（2）画出函数图像，数形结合得答案。

试题解析：(1)当x∈(-∞,0)时,-x∈(0,+∞),

∵y=f(x)是奇函数,

∴f(x)=-f(-x)=-[(-x)2-2(-x)]=-x2-2x,

∴f(x)=

(2)当x∈[0,+∞)时,f(x)=x2-2x=(x-1)2-1,最小值为-1.

∴当x∈(-∞,0)时,f(x)=-x2-2x=1-(x+1)2,最大值为1.

∴据此可作出函数y=f(x)的图象,如图所示,

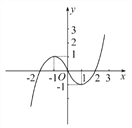
根据图象得,若方程f(x)=a恰有3个不同的解,则a的取值范围是(-1,1).