题目内容

函数f（x）=asinωx+bcosωx+1最小正周期为π，最大值为3，且f(
π
6
)=
3
+1(ab≠0），求f （x）的解析式．
f（x）=asinωx+bcosωx+1=
a2+b2
sin(ωx+?)+1
又最小正周期为π，最大值为3，且f(
π
6
)=
3
+1(ab≠0），
故
2π
ω
=π，ω=2，
a2+b2
+1=3，asin
π
6
+bcos
π
6
+1=
3
+1
解得a=1，b=
3

因此f(x)=sin2x+
3
cos2x+1
练习册系列答案
相关题目
有两个函数f（x）=asin（kx+
π
3
），g（x）=btan（kx-
π
3
）（k＞0），它们的周期之和为
3
2
π且f（
π
2
）=g（
π
2
），f(
π
4
)=-
3
g(
π
4
)+1求这两个函数，并求g（x）的单调递增区间．
如图，是函数f（x）=Asin（φx+φ）（其中A＞0，φ＞0，0＜φ＜π）的部分图象，则其解析为
y=2sin（
1
2
x+
3π
4
)
y=2sin（
1
2
x+
3π
4
)
．
已知函数f（x）=Asin（ωx+φ），x∈R（其中A＞0，ω＞0，0＜φ＜
π
2
）的图象与X轴的交点中，相邻两个交点之间的距离为
π
2
，且图象上一个最低点为M（
2π
3
，-2）
（Ⅰ）求f（x）的解析式．
（Ⅱ）求函教f（x）单调递减区间．
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
π2
，x∈R）的图象的一部分如图所示：
（1）求函数f（x）的解析式；
（2）求函数f（x）图象的对称轴方程．
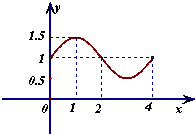精英家教网函数f（x）=Asin（ωx+φ）+b的图象如图，则f（x）的解析式和S=f（0）+f（1）+f（2）+…+f（2008）的值分别为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网