题目内容
已知一正2n（n≥4）边形，其顶点依次为A1，A2，…，A2n，平面上任取一点P0，设P0关于A1的对称点为P1，P1关于A2的对称点为P2，…，P2n-1关于A2n的对称点为P2n，则向量
等于（ ）
| P0P2n |
分析：由已知，Pi关于Ai+1的对称点为Pi+1，得出
=2
=2
（i=0，1，2，3），由向量加法的三角形法则，将向量
写成
+
+
+
+…+
再代入化简整理即可．
| PiPi+1 |
| PiAi+1 |
| Ai+1Pi+1 |
| P0P2n |
| P0P1 |
| P1P2 |
| P2P3 |
| P3P4 |
| P2n-1P2n |
解答：解：由已知，Pi关于Ai+1的对称点为Pi+1，
∴
=2
=2
∴
=
+
+
+
+…+
=2（
+
）+2（
+
）+…+2（
+
）
=2
+2
+…+2
=
故选：D
∴
| PiPi+1 |
| PiAi+1 |
| Ai+1Pi+1 |
∴
| P0P2n |
| P0P1 |
| P1P2 |
| P2P3 |
| P3P4 |
| P2n-1P2n |
=2（
| A1P1 |
| P1A2 |
| A3P3 |
| P3A4 |
| A2n-1P2n-1 |
| P2n-1A2n |
=2
| A1A2 |
| A3A4 |
| A2n-1A2n |
| 0 |
故选：D
点评：本题考查向量的运算，考查转化、计算能力，分析出
=2
=2
是解题的关键
| PiPi+1 |
| PiAi+1 |
| Ai+1Pi+1 |
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
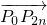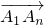
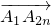
等于
等于（ ）
