Question

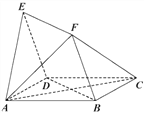
【题目】如图，已知抛物线与轴相交于点，两点，是该抛物线上位于第一象限内的点.

（Ⅰ） 记直线的斜率分别为，求证：为定值；

（Ⅱ）过点作，垂足为.若关于轴的对称点恰好在直线上，求的面积.

Answer 1

【答案】（Ⅰ）证明见解析（Ⅱ）

【解析】

（Ⅰ）由题意写出的坐标，设，，分别表示出，计算即可；

（Ⅱ）由题知直线的斜率为，由得，从而求解得到点的坐标及直线和的方程，联立得点坐标，根据三角形面积公式求出即可.

（Ⅰ）令，则，解得，

点，的坐标分别为，，

是该抛物线上位于第一象限内的点，

设点，，

，，

，即为定值.

（Ⅱ）关于轴的对称点恰好在直线上，

直线关于轴对称，

，

，

，即，

解得（负值舍去），

，，，

直线方程为，直线方程，

联立直线与的方程，

则，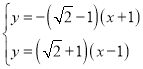

解得，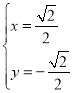

，

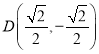的面积.