题目内容
如图,在△ 中,
中, 是
是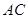 的中点,
的中点,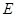 是
是 的中点,
的中点, 的延长线交
的延长线交 于
于 .
.

(Ⅰ)求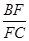 的值;(4分)
的值;(4分)
(Ⅱ)若△ 的面积为
的面积为 ,
四边形
,
四边形 的面积为
的面积为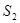 ,求
,求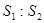 的值.
(6分)
的值.
(6分)
【答案】
证明:(Ⅰ)过D点作DG∥BC,并交AF于G点,
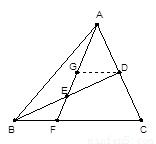
∵E是BD的中点,∴BE=DE,
又∵∠EBF=∠EDG,∠BEF=∠DEG,
∴△BEF≌△DEG,则BF=DG, ∴BF: FC=DG:FC, 又∵D是AC的中点,则DG:FC=1:2, 则BF:FC=1:2;即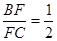 (4分)
(4分)
(Ⅱ)若△BEF以BF为底,△BDC以BC为底,则由(1)知BF:BC=1:3,又由BE:BD=1:2可知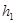 :
: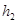 =1:2,其中
=1:2,其中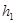 、
、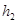 分别为△BEF和△BDC的高,则
分别为△BEF和△BDC的高,则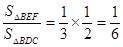 ,则
,则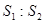 =1:5.(10分)
=1:5.(10分)
【解析】(I)过D作GD//BF,并交AF于G点,则易知BF=GD,所以本题转化为求DG:FC的值.
(II)本题可转化为求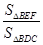 ,然后△BEF以BF为底,△BDC以BC为底,则由(1)知BF:BC=1:3,又由BE:BD=1:2可知
,然后△BEF以BF为底,△BDC以BC为底,则由(1)知BF:BC=1:3,又由BE:BD=1:2可知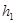 :
: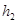 =1:2,问题到此基本得以解决
=1:2,问题到此基本得以解决

练习册系列答案
相关题目

 中,
中,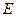 是
是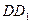 的中点,
的中点,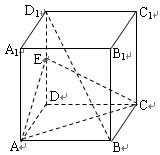
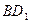 ∥平面
∥平面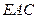 ;
;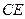 所成角的余弦值.
所成角的余弦值. 中,
中, 是
是 的中点.
的中点.
 平面
平面 ;
; 平面
平面 中,
中, 是
是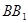 的中点。
的中点。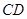 上求一点
上求一点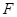 ,使
,使 平面
平面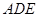 ;
;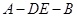 的余弦值.
的余弦值.
 中,
中, 是
是 的中点,将
的中点,将 沿
沿 折起,使点
折起,使点 到点
到点 的位置,使二面角
的位置,使二面角 的大小为
的大小为
 ;
; 与平面
与平面 所成角的正弦值
所成角的正弦值