题目内容
已知
=
,求cos4θ-sin4θ的值.
| 4sinθ-2cosθ |
| 5cosθ+3sinθ |
| 6 |
| 11 |
考点:同角三角函数基本关系的运用
专题:计算题
分析:已知等式左边分子分母除以cosθ,利用同角三角函数间基本关系化简求出tanθ的值,原式利用平方差公式化简,再利用二倍角的余弦函数公式及万能公式变形,将tanθ的值代入计算即可求出值.
解答:
解:已知等式变形得:
=
,
整理得:tanθ=2,
则原式=(cos2θ-sin2θ)(cos2θ+sin2θ)=cos2θ-sin2θ=cos2θ=
=
=-
.
| 4tanθ-2 |
| 5+3tanθ |
| 6 |
| 11 |
整理得:tanθ=2,
则原式=(cos2θ-sin2θ)(cos2θ+sin2θ)=cos2θ-sin2θ=cos2θ=
| 1-tan2θ |
| 1+tan2θ |
| 1-4 |
| 1+4 |
| 3 |
| 5 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
若函数f(x)=ax3+bx2+cx+d的图象如图所示,则一定有( )
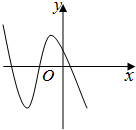

| A、b>0,c>0 |
| B、b<0,c>0 |
| C、b>0,c<0 |
| D、b<0,c<0 |
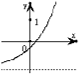
函数f(x)=
的定义域为( )
| ln(4-2x) | ||
|
| A、(-3,2) |
| B、[-3,2) |
| C、[-3,+∞) |
| D、(-∞,2) |
设复数z=-
+
i,则
的值为( )
| 1 |
| 2 |
| ||
| 2 |
| |z| |
| z |
A、-
| ||||||
B、-
| ||||||
C、
| ||||||
D、
|
如图,M是三棱锥P-ABC的底面△ABC的重心,若
=x
+y
+z
,则x+y-z的值为( )
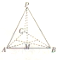
| PM |
| PA |
| PB |
| PC |

A、
| ||
B、
| ||
C、
| ||
| D、1 |
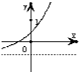
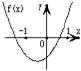 函数f(x)=(x-a)(x-b)(其中a>b)的图象如图所示,则函数g(x)=ax+b的大致图象是( )
函数f(x)=(x-a)(x-b)(其中a>b)的图象如图所示,则函数g(x)=ax+b的大致图象是( )