题目内容
P正三角形ABC所在平面外一点,PA=PB=PC= ,且PA,PB,PC两两垂直,则P到面ABC的距离为( )
,且PA,PB,PC两两垂直,则P到面ABC的距离为( )
A. | B. | C.1 | D. |
C
解析试题分析: 先根据题意,由于P正三角形ABC所在平面外一点,PA=PB=PC= ,且PA,PB,PC两两垂直,故可知点P在底面的射影为底面的垂心,即为底面的重心,那么利用正三角形的性质可知,底面的边长为
,且PA,PB,PC两两垂直,故可知点P在底面的射影为底面的垂心,即为底面的重心,那么利用正三角形的性质可知,底面的边长为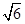 ,则底面的高线长为
,则底面的高线长为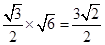 ,利用勾股定理可知P到面ABC的距离为1,选C.
,利用勾股定理可知P到面ABC的距离为1,选C.
考点:本题主要考查了空间中点到面的距离的求解问题。
点评:解决该试题的关键是画出图形,过P作底面ABC 的垂线,垂足为O,连接CO并延长交AB于E,说明PO为所求

练习册系列答案
相关题目
已知直线 、
、 、
、 不重合,平面
不重合,平面 、
、 不重合,下列命题正确的是( )
不重合,下列命题正确的是( )
A.若 , , , , ,则 ,则 |
B.若 , , ,则 ,则 |
C.若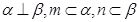 ,则 ,则 |
D.若 ,则 ,则 |
( )已知两个不同的平面 、
、 ,能判定
,能判定 //
// 的条件是
的条件是
A. 、 、 分别平行于直线 分别平行于直线 | B. 、 、 分别垂直于直线 分别垂直于直线 |
C. 、 、 分别垂直于平面 分别垂直于平面 | D. 内有两条直线分别平行于 内有两条直线分别平行于 |
设 为三条不同的直线,
为三条不同的直线, 为一个平面,下列命题中不正确的是( )
为一个平面,下列命题中不正确的是( )
A.若 ,则 ,则 与 与 相交 相交 |
B.若 则 则 |
C.若  // //  , , // //  , , ,则 ,则 |
D.若 // //  , , , , ,则 ,则 // //  |
如图, 所在的平面
所在的平面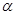 和四边形
和四边形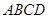 所在的平面
所在的平面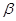 互相垂直,且
互相垂直,且 ,
,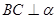 ,
,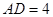 ,
,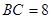 ,
,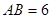 .若
.若 ,则动点
,则动点 在平面
在平面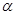 内的轨迹是
内的轨迹是 
| A.椭圆的一部分 | B.线段 | C.双曲线的一部分 | D.以上都不是 |
垂直于同一平面的两条直线一定( )
| A.相交 | B.平行 | C.异面 | D.以上都有可能 |
用 、
、 、
、 表示三条不同的直线,
表示三条不同的直线, 表示平面,给出下列命题:
表示平面,给出下列命题:
①若 ∥
∥ ,
, ∥
∥ ,则
,则 ∥
∥ ;②若
;②若 ⊥
⊥ ,
, ⊥
⊥ ,则
,则 ⊥
⊥ ;
;
③若 ∥
∥ ,
, ∥
∥ ,则
,则 ∥
∥ ;④若
;④若 ⊥
⊥ ,
, ⊥
⊥ ,则
,则 ∥
∥ ;则其中正确的是( )
;则其中正确的是( )
| A.①② | B.②③ | C.①④ | D.③④ |
三棱锥 的高为
的高为 ,若三个侧面两两垂直,则
,若三个侧面两两垂直,则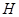 为△
为△ 的( )
的( )
| A.内心 | B.外心 | C.垂心 | D.重心 |
 =
= =
= ,则( )
,则( )