题目内容
(本题12分)已知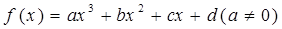 是定义在R上的函数, 且
是定义在R上的函数, 且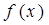 在(-1,0)和(4,5)上有相同的单调性,在(0,2)和(4,5)上
在(-1,0)和(4,5)上有相同的单调性,在(0,2)和(4,5)上
有相反的单调性.
(1) 求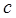 的值;
的值;
(2) 在函数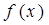 的图象上是否存在一点
的图象上是否存在一点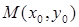 ,使得
,使得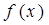 在点
在点 的
的
切线斜率为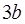 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】
0, 故符合题意的点不存在
【解析】解:(1) 因为 在(-1,0)和(0,2)上有相反的单调性,
在(-1,0)和(0,2)上有相反的单调性,
所以 是
是 的一个极值点,故
的一个极值点,故 ,
,
即
 有一个解
有一个解 ,则
,则
(2) 令 ,得
,得 ,解得:
,解得:
因为 在(0,2)和(4,5)上有相反的单调性,
在(0,2)和(4,5)上有相反的单调性,
所以 ,即
,即 ,则
,则
假设存在点 ,则
,则 ,即
,即
由于
故符合题意的点不存在。

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
 ,顶点为O,动直线
,顶点为O,动直线 与抛物
与抛物 交于
交于 、
、 两点
两点 是一个与
是一个与 无关的常数;
无关的常数; 的点
的点 的轨迹方程。
的轨迹方程。

 ,
, 
 是平面上的一组基底,若
是平面上的一组基底,若



 ,
, 的值;
的值; 的单位向量,当
的单位向量,当 时,求
时,求 的最大值。
的最大值。