题目内容
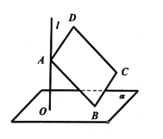
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.首届中国国际进口博览会的某展馆棚顶一角的钢结构可以抽象为空间图形阳马.如图所示,在阳马![]() 中,
中,![]() 底面
底面![]() .
.
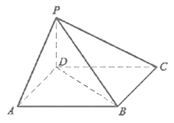
(1)若![]() ,斜梁
,斜梁![]() 与底面
与底面![]() 所成角为
所成角为![]() ,求立柱
,求立柱![]() 的长(精确到
的长(精确到![]() );
);
(2)证明:四面体![]() 为鳖臑;
为鳖臑;
(3)若![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一个动点,求
上一个动点,求![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() .
.
【解析】
(1)推导出侧棱![]() 在平面
在平面![]() 上的射影是
上的射影是![]() ,从而
,从而![]() 是侧棱
是侧棱![]() 与平面
与平面![]() 所成角,
所成角,![]() ,从而求得立柱
,从而求得立柱![]() 的长.
的长.
(2)四边形![]() 是长方形,从而
是长方形,从而![]() 是直角三角形,由此得出
是直角三角形,由此得出![]() ,从而三角形
,从而三角形![]() 是直角三角形,由
是直角三角形,由![]() 平面
平面![]() ,得
,得![]() 是直角三角形,由此能证明四面体
是直角三角形,由此能证明四面体![]() 为鳖臑.
为鳖臑.
(3)利用转化法求出异面直线![]() 与
与![]() 的距离,即可求得三角形
的距离,即可求得三角形![]() 面积的最小值.
面积的最小值.
(1)因为侧棱![]() 平面
平面![]() ,所以侧棱
,所以侧棱![]() 在底面
在底面![]() 上的射影是
上的射影是![]() ,所以
,所以![]() 是侧棱
是侧棱![]() 与平面
与平面![]() 所成角,所以
所成角,所以![]() ,在
,在![]() 中,
中,![]() ,所以
,所以![]() ,即
,即![]() ,
,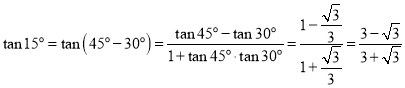 ,所以
,所以![]() .
.
(2)证明:由题意知四边形![]() 是长方形,所以三角形
是长方形,所以三角形![]() 是直角三角形.
是直角三角形.
由于![]() 平面
平面![]() ,所以
,所以![]() ,所以三角形
,所以三角形![]() 和三角形
和三角形![]() 是直角三角形.因为
是直角三角形.因为![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() ,所以三角形
,所以三角形![]() 是直角三角形.所以四面体
是直角三角形.所以四面体![]() 为鳖臑.
为鳖臑.
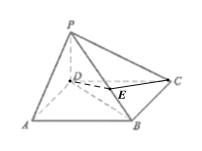
(3)![]() 与
与![]() 是两异面直线,
是两异面直线,![]() ,所以
,所以![]() 平面
平面![]() ,则两异面直线
,则两异面直线![]() 与
与![]() 的距离等于
的距离等于![]() 到平面
到平面![]() 的距离,也即
的距离,也即![]() 到平面
到平面![]() 的距离,等于
的距离,等于![]() 到直线
到直线![]() 的距离.因为
的距离.因为![]() ,所以
,所以![]() ,则
,则![]() 到
到![]() 的距离为
的距离为![]() .
.
所以线段![]() 上的动点
上的动点![]() 到
到![]() 的最小距离为
的最小距离为![]() .则三角形
.则三角形![]() 面积的最小值为
面积的最小值为![]() .
.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目