题目内容
设a，b是互不相等的正数，则在三个不等式①| 1 |
| a+1 |
| 1 |
| a-b |
| b |
| a2 |
| a |
| b2 |
| 1 |
| a |
| 1 |
| b |
分析：根据题意，①③采用作差变形，判断其符号，从而得出结论，对于②，简单的方法是取特殊值检验其正确性．
解答：解：①
-(1-a)=
=
=
＞0，∴
＞1-a，∴①成立；
②令a=1，b=2，可知不等式不成立，∴②不成立；
③
+
-(
+
)=(
-
)+(
-
)=
+
=
=
≥0，∴
+
≥
+
，∴③成立．
| 1 |
| a+1 |
| 1-(1+a)(1-a) |
| a+1 |
| 1-(1-a2) |
| a+1 |
| a2 |
| a+1 |
| 1 |
| a+1 |
②令a=1，b=2，可知不等式不成立，∴②不成立；
③
| b |
| a2 |
| a |
| b2 |
| 1 |
| a |
| 1 |
| b |
| b |
| a2 |
| 1 |
| a |
| a |
| b2 |
| 1 |
| b |
| b-a |
| a2 |
| a-b |
| b2 |
| (a-b)(a2-b2) |
| a2b2 |
| (a-b)2(a+b) |
| a2b2 |
| b |
| a2 |
| a |
| b2 |
| 1 |
| a |
| 1 |
| b |
点评：本题考查用不等式的性质及作差法判断数的大小，并采用特殊值检验的方法排除错误的选项．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
．
，②
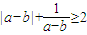，③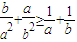
中恒成立的是 （把你认为正确的答案的序号都填上）．