题目内容
已知
，分别求：sin（α+β），cos（α-β），tan（α-β）的值．
解：∵sinα=
，α∈（
，π），∴cosα=-
；
又cosβ=-
，β∈（π，
），∴sinβ=-
．
∴sin（α+β）=sinαcosβ+cosαsinβ=×（-）+（-）×（-）=
；
sin（α-β）=sinαcosβ-cosαsinβ=×（-）-（-）×（-）=-
，
cos（α-β）=cosαcosβ+sinαsinβ=（-）×（-）+×（-）=-
；
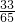∴tan（α-β）=
=
．
分析：依题意可求得cosα，sinβ，利用两角和与两角差的正弦、余弦与正切公式即可求得sin（α+β），cos（α-β），tan（α-β）的值．
点评：本题考查两角和与两角差的正弦、余弦与正切公式，求得cosα，sinβ的值是关键，属于中档题．
，α∈（，π），∴cosα=-；又cosβ=-
，β∈（π，），∴sinβ=-．∴sin（α+β）=sinαcosβ+cosαsinβ=
×（-）+（-）×（-）=；sin（α-β）=sinαcosβ-cosαsinβ=
×（-）-（-）×（-）=-，cos（α-β）=cosαcosβ+sinαsinβ=（-
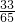）×（-）+×（-）=-；∴tan（α-β）=
=．分析：依题意可求得cosα，sinβ，利用两角和与两角差的正弦、余弦与正切公式即可求得sin（α+β），cos（α-β），tan（α-β）的值．
点评：本题考查两角和与两角差的正弦、余弦与正切公式，求得cosα，sinβ的值是关键，属于中档题．
练习册系列答案
相关题目
，分别求：sin（α+β），cos（α-β），tan（α-β）的值．
，分别求：sin（α+β），cos（α-β），tan（α-β）的值．
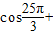
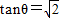，分别求下列各式的值：
；