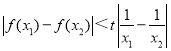题目内容
【题目】已知函数![]() 有两个零点
有两个零点![]() 、
、![]() ,
,![]() ,则下面说法不正确的是( )
,则下面说法不正确的是( )
A.![]() B.
B.![]()
C.![]() D.有极小值点
D.有极小值点![]() ,且
,且![]()
【答案】C
【解析】
先证明出对数平均不等式![]() ,由题意得出
,由题意得出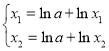 ,将两式作差结合对数平均不等式可判断出A、B选项的正误,利用导数分析函数
,将两式作差结合对数平均不等式可判断出A、B选项的正误,利用导数分析函数![]() 的单调性,结合该函数的极值以及该函数有两个零点可判断出选项的正误,求出极值点,将
的单调性,结合该函数的极值以及该函数有两个零点可判断出选项的正误,求出极值点,将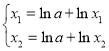 中两等式相加可判断D选项的正误.
中两等式相加可判断D选项的正误.
先证明对数平均不等式![]() .
.
先考虑不等式![]() ,设
,设![]() ,
,
即证![]() ,即证
,即证![]() ,令
,令![]() ,即证不等式
,即证不等式![]() .
.
构造函数![]() ,则
,则![]() ,
,
所以,函数![]() 在
在![]() 上单调递增,则
上单调递增,则![]() ,
,
![]() 当
当![]() ,
,![]() 且
且![]() 时,
时,![]() ;
;
接下来考虑不等式![]() ,设
,设![]() ,
,
即证![]() ,即证
,即证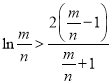 ,设
,设![]() ,即证不等式
,即证不等式![]() .
.
构造函数![]() ,则
,则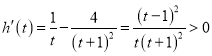 ,
,
所以,函数![]() 在
在![]() 上单调递增,则
上单调递增,则![]() ,
,
![]() 当
当![]() ,
,![]() 且
且![]() 时,有
时,有![]() .
.
即当![]() ,
,![]() 且
且![]() 时,
时,![]() .
.
对于C选项,![]() ,
,![]() .
.
①当![]() 时,
时,![]() 对于任意
对于任意![]() 恒成立,此时函数
恒成立,此时函数![]() 在
在![]() 上单调递增,该函数最多有一个零点;
上单调递增,该函数最多有一个零点;
②当![]() 时,令
时,令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
所以,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
所以,函数![]() 在
在![]() 处取得极小值,
处取得极小值,
由于该函数有两个零点,则![]() ,
,
即![]() ,解得
,解得![]() ,C选项错误;
,C选项错误;
对于A、B选项,由于函数![]() 有两个零点
有两个零点![]() 、
、![]() ,且
,且![]() ,
,
由于![]() ,则
,则![]() ,
,![]() ,且有
,且有![]() ,
,
则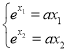 ,两个等式两边取自然对数得
,两个等式两边取自然对数得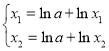 ,
,
两式相减得![]() ,
,![]() ,
,
由对数平均不等式得![]() ,即
,即![]() ,
,
![]() ,
,![]() ,A、B选项都正确;
,A、B选项都正确;
对于D选项,由C选项可知,![]() ,
,
将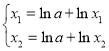 中两个等式相加得
中两个等式相加得![]() ,
,
![]() ,即
,即![]() ,D选项正确.
,D选项正确.
故选:C.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目