Question

【题目】在平面直角坐标系中，点到两点、的距离之和等于，设点的轨迹为，斜率为的直线过点，且与轨迹交于、两点.

（1）写出轨迹的方程；

（2）如果，求的值；

（3）是否存在直线，使得在直线上存在点，满足为等边三角形？若存在，求出直线的方程；若不存在，说明理由.

Answer 1

【答案】（1）；（2）；（3）存在直线:，使得在直线上存在点，满足为等边三角形；

【解析】

(1)根据点到两点、的距离之和等于,且,可知轨迹为椭圆,由,求得,从而可得椭圆方程;

(2)联立直线与椭圆,根据弦长公式求出弦长与已知弦长相等,可求出直线斜率;

(3) 将为等边三角形,转化为且,利用(2)的弦长以及两点间的距离公式可求得答案.

(1) 因为点到两点、的距离之和等于,且,

所以点的轨迹是,以、为焦点的椭圆,且,

所以,

所以轨迹的方程为:.

(2) 直线的方程为:,将其代入到,

整理得,

设,

则,,

所以

,

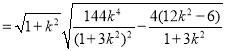
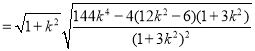
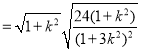
所以,即,所以.

(3)假设存在点满足题意,

设的中点为,

由(1)知,

, ,

因为为等边三角形,所以且,

所以, ,

所以,化简得,所以,

所以存在直线:，使得在直线上存在点，满足为等边三角形