题目内容
已知向量 =(sin(ωx+φ),2),
=(sin(ωx+φ),2), =(1,cos(ωx+φ)),ω>0,0<φ<
=(1,cos(ωx+φ)),ω>0,0<φ< .函数f(x)=(
.函数f(x)=( +
+ )•(
)•( -
- ),若y=f(x)的图象的一个对称中心与它相邻的一个对称轴之间的距离为1,且过点M(1,
),若y=f(x)的图象的一个对称中心与它相邻的一个对称轴之间的距离为1,且过点M(1, ).
).
(Ⅰ)求函数f(x)的表达式;
(Ⅱ)当-1≤x≤1时,求函数f(x)的单调区间.
解:(1)f(x)=( +
+ )•(
)•( -
- )=
)=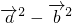 =sin2(ωx+φ)+4-1-cos2(ωx+φ),
=sin2(ωx+φ)+4-1-cos2(ωx+φ),
=-cos(2ωx+2φ)+3
由题意得周期T= =4,故ω=
=4,故ω= …(4分)
…(4分)
又图象过点M(1, ),所以
),所以 =3-cos(
=3-cos( +2φ)
+2φ)
即sin2φ= ,而0<φ<
,而0<φ< ,所以2φ=
,所以2φ=
∴f(x)=3-cos( x+
x+ )
)
(2)当-1≤x≤1时,- ≤
≤ x+
x+ ≤
≤
∴当- ≤
≤ x+
x+ ≤0时,即x∈[-1,-
≤0时,即x∈[-1,- ]时,f(x)是减函数
]时,f(x)是减函数
当0≤ x+
x+ ≤
≤ 时,即x∈[-
时,即x∈[- ,1]时,f(x)是增函数
,1]时,f(x)是增函数
∴函数f(x)的单调减区间是[-1,- ],单调增区间是[-
],单调增区间是[- ,1]
,1]
分析:(Ⅰ)首先由向量运算以及三角恒等变换化简f(x)=( +
+ )•(
)•( -
- )=-cos(2ωx+2φ)+3,再由y=f(x)的图象的一个对称中心与它相邻的一个对称轴之间的距离为1判断出函数的周期是4,由周期公式求得ω,再由图象过点M(1,
)=-cos(2ωx+2φ)+3,再由y=f(x)的图象的一个对称中心与它相邻的一个对称轴之间的距离为1判断出函数的周期是4,由周期公式求得ω,再由图象过点M(1, ),代入求得φ,即得函数f(x)的表达式.
),代入求得φ,即得函数f(x)的表达式.
(Ⅱ)当-1≤x≤1时,代入求得相位的取值范围结合余弦函数的单调性求函数f(x)的单调区间.
点评:本题考查余弦函数的单调性,求解本题的关键是进行正确的向量的坐标运算与三角恒等变换求出函数的解析式,再根据余弦函数的单调性求出函数的单调区间.
 +
+ )•(
)•( -
- )=
)=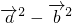 =sin2(ωx+φ)+4-1-cos2(ωx+φ),
=sin2(ωx+φ)+4-1-cos2(ωx+φ),=-cos(2ωx+2φ)+3
由题意得周期T=
 =4,故ω=
=4,故ω= …(4分)
…(4分)又图象过点M(1,
 ),所以
),所以 =3-cos(
=3-cos( +2φ)
+2φ)即sin2φ=
 ,而0<φ<
,而0<φ< ,所以2φ=
,所以2φ=
∴f(x)=3-cos(
 x+
x+ )
)(2)当-1≤x≤1时,-
 ≤
≤ x+
x+ ≤
≤
∴当-
 ≤
≤ x+
x+ ≤0时,即x∈[-1,-
≤0时,即x∈[-1,- ]时,f(x)是减函数
]时,f(x)是减函数当0≤
 x+
x+ ≤
≤ 时,即x∈[-
时,即x∈[- ,1]时,f(x)是增函数
,1]时,f(x)是增函数∴函数f(x)的单调减区间是[-1,-
 ],单调增区间是[-
],单调增区间是[- ,1]
,1]分析:(Ⅰ)首先由向量运算以及三角恒等变换化简f(x)=(
 +
+ )•(
)•( -
- )=-cos(2ωx+2φ)+3,再由y=f(x)的图象的一个对称中心与它相邻的一个对称轴之间的距离为1判断出函数的周期是4,由周期公式求得ω,再由图象过点M(1,
)=-cos(2ωx+2φ)+3,再由y=f(x)的图象的一个对称中心与它相邻的一个对称轴之间的距离为1判断出函数的周期是4,由周期公式求得ω,再由图象过点M(1, ),代入求得φ,即得函数f(x)的表达式.
),代入求得φ,即得函数f(x)的表达式.(Ⅱ)当-1≤x≤1时,代入求得相位的取值范围结合余弦函数的单调性求函数f(x)的单调区间.
点评:本题考查余弦函数的单调性,求解本题的关键是进行正确的向量的坐标运算与三角恒等变换求出函数的解析式,再根据余弦函数的单调性求出函数的单调区间.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目