题目内容
设△ABC的内角A，B，C所对的边分别为a，b，c，且a+c=6，b=2，cosB=
．（Ⅰ）求a，c的值；
（Ⅱ）求△ABC的面积．
【答案】分析：（Ⅰ）△ABC中，a+c=6，b=2，cosB=
，由余弦定理可得 ac=9，由此解得a、c的值．
（Ⅱ）根据△ABC的面积为
ac•sinB，运算求得结果．
解答：解：（Ⅰ）△ABC中，a+c=6，b=2，cosB=
，则由余弦定理可得
b2=4=a2+c2-2ac•cosB=a2+c2-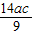
=（a+c）2-
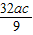，∴ac=9．
解得a=c=3．
（Ⅱ）△ABC的面积为
ac•sinB=
×9×
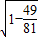=2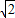
．
点评：本题主要考查余弦定理、三角形的面积公式的应用，属于中档题．
，由余弦定理可得 ac=9，由此解得a、c的值．（Ⅱ）根据△ABC的面积为
ac•sinB，运算求得结果．解答：解：（Ⅰ）△ABC中，a+c=6，b=2，cosB=
，则由余弦定理可得b2=4=a2+c2-2ac•cosB=a2+c2-
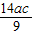=（a+c）2-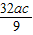，∴ac=9．解得a=c=3．
（Ⅱ）△ABC的面积为
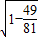ac•sinB=×9×=2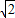．点评：本题主要考查余弦定理、三角形的面积公式的应用，属于中档题．
练习册系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目