题目内容
平面直角坐标系中,O为坐标原点,给定两点A(1,0),B(0,一2),点C满足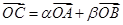 ,其中
,其中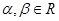 ,且
,且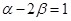 .
.
(1)求点C的轨迹方程;
(2)设点C的轨迹与椭圆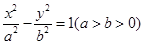 交于两点M,N,且以MN为直径的圆过原点,求证:
交于两点M,N,且以MN为直径的圆过原点,求证: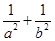 为定值;
为定值;
(3)在(2)的条件下,若椭圆的离心率不大于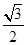 ,求椭圆长轴长的取值范围。
,求椭圆长轴长的取值范围。
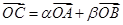 ,其中
,其中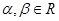 ,且
,且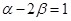 .
.(1)求点C的轨迹方程;
(2)设点C的轨迹与椭圆
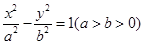 交于两点M,N,且以MN为直径的圆过原点,求证:
交于两点M,N,且以MN为直径的圆过原点,求证: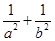 为定值;
为定值;(3)在(2)的条件下,若椭圆的离心率不大于
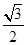 ,求椭圆长轴长的取值范围。
,求椭圆长轴长的取值范围。(1) 。
。
(2)由
以MN为直径的圆过原点O,
 为定值。
为定值。
(3)椭圆长轴的取值范围是 。
。
 。
。(2)由

以MN为直径的圆过原点O,

 为定值。
为定值。(3)椭圆长轴的取值范围是
 。
。试题分析:(1)设
 ,由
,由 可得
可得

有
 ,即点C的轨迹方程为
,即点C的轨迹方程为 4分
4分(2)由

设

则

∵以MN为直径的圆过原点O,


 为定值 9分
为定值 9分(3)




∴椭圆长轴的取值范围是
 12分
12分点评:中档题,本题求轨迹方程,主要运用的是平面向量的线性运算及向量的坐标运算和向量的相等。研究直线与圆锥曲线的位置关系,往往应用韦达定理,通过“整体代换”,简化解题过程,实现解题目的。

练习册系列答案
相关题目
 ,
, 满足
满足 ,且
,且 ,则向量
,则向量



 中,
中, 点
点 是边
是边 的中点,则
的中点,则 等于_______.
等于_______. 满足
满足 ,则
,则

 ( )
( )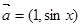 ,
, ,函数
,函数
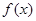 的解析式及其单调递增区间;
的解析式及其单调递增区间; 中,角
中,角 为钝角,若
为钝角,若 ,
, ,
, .求
.求 =(2,-1),
=(2,-1), =(x,-2),
=(x,-2), =(3,y),若
=(3,y),若 的模为________.
的模为________. ,则
,则 = .
= .  满足
满足 的夹角为60°,若
的夹角为60°,若 则实数
则实数 的值为 。
的值为 。