题目内容
点（x，y）在直线x+3y-2=0上，则3x+27y+3取值范围为 ．
【答案】分析：根据题意用x=2-3y代入，可得3x+27y=9×（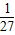
）y+27y，再利用基本不等式得3x+27y≥6，从而得3x+27y+3的最小值为9，得到所求取值范围．
解答：解：∵点（x，y）在直线x+3y-2=0上，可得x=2-3y
∴3x+27y=32-3y+27y=9×（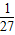
）y+27y≥2
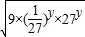=6
由此可得：3x+27y+3≥6+3=9
即3x+27y+3的取值范围是[9，+∞）
故答案为：[9，+∞）
点评：本题给出指数式，求该式的取值范围，着重考查了指数的运算性质和利用基本不等式求最值等知识，属于中档题．
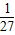）y+27y，再利用基本不等式得3x+27y≥6，从而得3x+27y+3的最小值为9，得到所求取值范围．解答：解：∵点（x，y）在直线x+3y-2=0上，可得x=2-3y
∴3x+27y=32-3y+27y=9×（
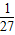）y+27y≥2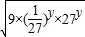=6由此可得：3x+27y+3≥6+3=9
即3x+27y+3的取值范围是[9，+∞）
故答案为：[9，+∞）
点评：本题给出指数式，求该式的取值范围，着重考查了指数的运算性质和利用基本不等式求最值等知识，属于中档题．
练习册系列答案
通城学典默写能手系列答案
相关题目
若平面上点（x，y）在直线x+2y=3上移动，则2x+4y的最小值是（ ）
A、
| |||
B、
| |||
C、
| |||
D、
|