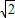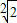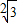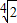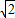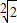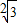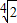Question

若平面上点（x，y）在直线x+2y=3上移动，则2^x+4^y的最小值是（　　）

• A、

  2

• B、

  2	2

• C、

  2	3

• D、

  4	2

Answer 1

分析：由于2^x•4^y=2^x+2y是常数，利用基本不等式求2^x+4^y的最小值．

解答：解：∵2x+4y≥2

2x•4y

=2

2x+2y

又∵x+2y=3
∴2x+4y≥2

2x•4y

=2

2x+2y

=2

23

=4

2

当且仅当2^x=4^y即x=2y=

3

2

时取等号
故选项为D

点评：本题考查利用基本不等式求函数的最值要注意满足：一正、二定、三相等．