题目内容
11.已知顶点为原点O,焦点在x轴上的抛物线,其内接△ABC的重心是焦点F,若直线BC的方程为4x+y-20=0.(1)求抛物线方程;
(2)过抛物线上一动点M作抛物线切线l,又MN⊥l且交抛物线于另一点N,ME(E在M的右侧)平行于x轴,若∠FMN=λ∠NME,求λ的值.
分析 (1)先设抛物线方程为y2=4px,然后表示出焦点坐标,抛物线和直线方程联立可消去y得到4x2-(p+40)x+100=0,进而可得到B,C的横坐标之和与纵坐标之和,再由A点在抛物线上得到坐标满足抛物线方程,最后将A,B,C的坐标代入△ABC重心坐标公式可求得p的值,从而确定抛物线方程;
(2)设M($\frac{{m}^{2}}{16}$,m),由y2=16x,两边对x求导,求得切线的斜率,再由两直线的到角公式可得tan∠FMN=tan∠NME,即可得到所求值.
解答 解:(1)设抛物线的方程为y2=4px,则其焦点为(p,0),
与直线方程4x+y-20=0联立,有(-4x+20)2=4px
∴4x2-(p+40)x+100=0,且y=-4x+20,
该方程的解为B,C两点的坐标(x2,y2),(x3,y3),
x2+x3=$\frac{p+40}{4}$(1)
y2+y3=-4(x2+x3)+40=-p (2)
设A(x1,y1),∵A在抛物线上
∴y12=4px1(3),
△ABC重心坐标为:($\frac{{x}_{1}+{x}_{2}+{x}_{3}}{3}$,$\frac{{y}_{1}+{y}_{2}+{y}_{3}}{3}$)
∵重心为抛物线焦点,
∴$\frac{{x}_{1}+{x}_{2}+{x}_{3}}{3}$=p,$\frac{{y}_{1}+{y}_{2}+{y}_{3}}{3}$=0,
将(1),(2)代入,得:
x1+$\frac{p+40}{4}$=3p,y1-p=0,
与(3)联立,三个方程,x1,y1,p三个未知数,
解得p=4,
故抛物线的方程为y2=16x;
(2)设M($\frac{{m}^{2}}{16}$,m),由y2=16x,两边对x求导,可得
2yy′=16,即有切线的斜率为k=$\frac{8}{m}$,
由两直线垂直可得MN的斜率为-$\frac{m}{8}$,
由F(4,0),
可得直线MF的斜率为$\frac{16m}{{m}^{2}-64}$,
由直线MN到直线MF的角的公式可得,
tan∠FMN=$\frac{\frac{16m}{{m}^{2}-64}+\frac{m}{8}}{1-\frac{16m}{{m}^{2}-64}•\frac{m}{8}}$=-$\frac{m}{8}$,
由题意可得tan∠FME=$\frac{m}{8}$,
由∠NME,∠FMN均为锐角,
则∠NME=∠FMN,
可得λ=1.
点评 本题主要考查抛物线的标准方程和直线与抛物线的联立问题,考查直线和抛物线相切的条件,注意运用导数,同时考查两直线的到角公式,考查运算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | -2015 | B. | 2015 | C. | 0 | D. | 2014 |
| A. | a+b | B. | a-b | C. | $\frac{a+b}{2}$ | D. | $\frac{a-b}{2}$ |
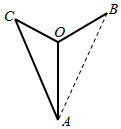 如图是某设计师设计的Y型饰品的平面图,其中支架OA,OB,OC两两成120°,OC=1,AB=OB+OC,且OA>OB,现设计师在支架OB上装点普通珠宝,普通珠宝的价值为M,且M与OB长成正比,比例系数为k(k为正常数):在△AOC区域(阴影区域)内镶嵌名贵珠宝,名贵珠宝的价值为N,且N与△AOC的面积成正比,比例系数为4$\sqrt{3}$k,设OA=x,OB=y.
如图是某设计师设计的Y型饰品的平面图,其中支架OA,OB,OC两两成120°,OC=1,AB=OB+OC,且OA>OB,现设计师在支架OB上装点普通珠宝,普通珠宝的价值为M,且M与OB长成正比,比例系数为k(k为正常数):在△AOC区域(阴影区域)内镶嵌名贵珠宝,名贵珠宝的价值为N,且N与△AOC的面积成正比,比例系数为4$\sqrt{3}$k,设OA=x,OB=y.