题目内容
分析在柱坐标系,球坐标系和空间直角坐标系中刻画空间中点的位置的方法,探讨有何异同?
探究:它们都是三维的坐标，球坐标与柱坐标都是在空间直角坐标基础上建立的.
在直角坐标中，需要三个长度：(x,y,z)，而在球坐标与柱坐标中，既需要长度，也需要角度.它们是从长度、方向来描述一个点的位置，需要(ρ,θ,z)或者(r,φ,θ).
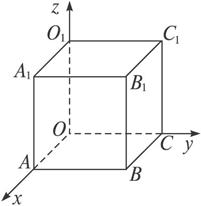
空间直角坐标：设点M为空间一已知点.我们过点M作三个平面分别垂直于x轴、y轴、z轴，它们与x轴、y轴、z轴的交点依次为P、Q、R，这三点在x轴、y轴、z轴的坐标依次为x、y、z.于是空间的一点M就唯一地确定了一个有序数组x，y，z.这组数x，y，z就叫做点M的坐标，并依次称x,y和z为点M的横坐标,纵坐标和竖坐标.(如图1-4-3所示）
图1-4-3
坐标为(x,y,z)的点M通常记为M(x,y,z).这样，通过空间直角坐标系，就建立了空间的点M和有序数组(x,y,z)之间的一一对应关系.
如果点M在yOz平面上，则x=0；同样，zOx面上的点，y=0；如果点M在x轴上，则y=z=0；如果M是原点，则x=y=z=0等.
几种三维坐标互相不同，互相有联系，互相能够转化,它们都是刻画空间一点的位置，只是描述的角度不同.
练习册系列答案
期末集结号系列答案
相关题目
,5)，则此长方体外接球的体积为________________.
