题目内容
设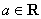 ,函数
,函数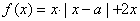 .
.
(1)若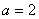 ,求函数
,求函数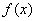 在区间
在区间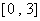 上的最大值;
上的最大值;
(2)若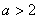 ,作函数
,作函数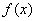 的图象并写出
的图象并写出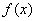 的单调区间(不必证明);
的单调区间(不必证明);
(3)若存在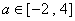 ,使得关于
,使得关于 的方程
的方程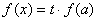 有三个不相等的实数解,求实数
有三个不相等的实数解,求实数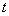 的取值范围.
的取值范围.
(1)当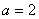 ,
, 时,
时,
作函数图像(图像略),可知函数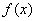 在区间
在区间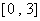 上是增函数,所以
上是增函数,所以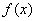 的最大值为
的最大值为 .
.
 (2)
(2)
①当 时,
时, ,
,
因为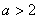 ,所以
,所以 ,所以
,所以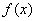 在
在 上单调递增.
上单调递增.
②当 时,
时,  ,
,
因为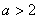 ,所以
,所以 ,所以
,所以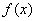 在
在 上单调递增,在
上单调递增,在 上单调递减.
上单调递减.
综上,函数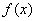 的单调递增区间是
的单调递增区间是 和
和 ,单调递减区间是
,单调递减区间是 .)
.)
(3)①当 时,
时, ,
, ,所以
,所以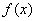 在
在 上是增函数,关于
上是增函数,关于 的方程
的方程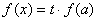 不可能有三个不相等的实数解.
不可能有三个不相等的实数解.
②当 时,由(1)知
时,由(1)知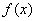 在
在 和
和 上分别是增函数,在
上分别是增函数,在 上是减函数,当且仅当
上是减函数,当且仅当 时,方程
时,方程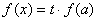 有三个不相等的实数解.
有三个不相等的实数解.
即 .令
.令 ,
, 在
在 时是增函数,故
时是增函数,故 .
.
所以,实数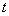 的取值范围是
的取值范围是 .
.

练习册系列答案
相关题目
 中,已知
中,已知 ,
, ,则
,则 的焦点为
的焦点为 ,
, 为抛物线上一点,过
为抛物线上一点,过 则
则 的面积为( )
的面积为( ) B.
B.  C. 6 D. 8
C. 6 D. 8 的导函数为
的导函数为 ,且
,且 ,则
,则 上的单调增区间为 ( )
上的单调增区间为 ( ) B.
B.  C.
C.  D.
D.  ,其导函数为
,其导函数为 ,则
,则 .
.  ,若
,若 ,且
,且 成等比数列,则此样本的平均数和中位数分别是 ( )
成等比数列,则此样本的平均数和中位数分别是 ( )  B.
B. C.
C.  D.
D.
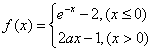 (
(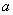 是常数且
是常数且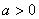 ).对于下列命题:
).对于下列命题: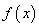 的最小值是
的最小值是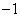 ;②函数
;②函数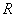 上是单调函数;③若
上是单调函数;③若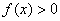 在
在 上恒成立,则
上恒成立,则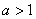 ;④对任意
;④对任意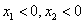 且
且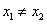 ,恒有
,恒有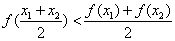 .其中正确命题的序号是 .
.其中正确命题的序号是 .  (
( 为常数,A>0,
为常数,A>0, >0)的部分图象如图所示,则
>0)的部分图象如图所示,则 的值是 .
的值是 . 
 ,则等于
,则等于 ( )
( ) B.
B. C.
C. D.
D.