题目内容
已知函数f(x)=x3-ax2+bx+c的图象为曲线E.
(1)若函数f(x)可以在x=-1和x=3时取得极值,求此时a,b的值;
(2)在满足(1)的条件下,f(x)<2c在x∈[-2,6]恒成立,求c的取值范围.
(1)若函数f(x)可以在x=-1和x=3时取得极值,求此时a,b的值;
(2)在满足(1)的条件下,f(x)<2c在x∈[-2,6]恒成立,求c的取值范围.
考点:利用导数研究函数的极值,导数在最大值、最小值问题中的应用
专题:导数的概念及应用
分析:(1)若函数f(x)可以在x=-1和x=3时取得极值,则f'(x)=3x2-2ax+b=0有两个解x=-1,x=3,易得a=3,b=-9.
(2)由(1)得f(x)=x3-3x2-9x+c,根据题意:c>x3-3x2-9x(x∈[-2,6])恒成立,令g(x)=x3-3x2-9x,令g′(x)=0,解得:x=-1,x=3,从而函数g(x)=x3-3x2-9x在[-2,-1)递增,(-1,3)递减,(3,6]递增,求出函数g(x)在x=-1时有极大值5且在端点x=6处的值为54,问题解决.
(2)由(1)得f(x)=x3-3x2-9x+c,根据题意:c>x3-3x2-9x(x∈[-2,6])恒成立,令g(x)=x3-3x2-9x,令g′(x)=0,解得:x=-1,x=3,从而函数g(x)=x3-3x2-9x在[-2,-1)递增,(-1,3)递减,(3,6]递增,求出函数g(x)在x=-1时有极大值5且在端点x=6处的值为54,问题解决.
解答:
解:(1)若函数f(x)可以在x=-1和x=3时取得极值,
则f'(x)=3x2-2ax+b=0有两个解x=-1,x=3,
易得a=3,b=-9.
(2)由(1)得f(x)=x3-3x2-9x+c,
根据题意:c>x3-3x2-9x(x∈[-2,6])恒成立,
令g(x)=x3-3x2-9x,
∴g′(x)=3x2-6x-9,
令g′(x)=0,解得:x=-1,x=3,
∴g(x)在(-∞,-1),(3,+∞)上递增,在(-1,3)递减,
∴函数g(x)=x3-3x2-9x在[-2,-1)递增,(-1,3)递减,(3,6]递增,
∴函数g(x)在x=-1时有极大值5且在端点x=6处的值为54,
∴函数g(x)=x3-3x2-9x(x∈[-2,6])的最大值为54,
∴c>54.
则f'(x)=3x2-2ax+b=0有两个解x=-1,x=3,
易得a=3,b=-9.
(2)由(1)得f(x)=x3-3x2-9x+c,
根据题意:c>x3-3x2-9x(x∈[-2,6])恒成立,
令g(x)=x3-3x2-9x,
∴g′(x)=3x2-6x-9,
令g′(x)=0,解得:x=-1,x=3,
∴g(x)在(-∞,-1),(3,+∞)上递增,在(-1,3)递减,
∴函数g(x)=x3-3x2-9x在[-2,-1)递增,(-1,3)递减,(3,6]递增,
∴函数g(x)在x=-1时有极大值5且在端点x=6处的值为54,
∴函数g(x)=x3-3x2-9x(x∈[-2,6])的最大值为54,
∴c>54.
点评:本题考察了函数的单调性,极值问题,导数的应用,是一道基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 椭圆C:
椭圆C: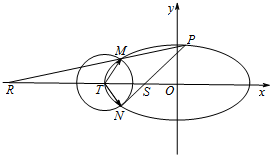 如图,已知椭圆C:
如图,已知椭圆C: