题目内容
已知等差数列{an}满足a2=0,a6+a8=-10
(1)求数列{an}的通项公式;
(2)求数列{ }的前n项和.
}的前n项和.
(1)求数列{an}的通项公式;
(2)求数列{
 }的前n项和.
}的前n项和.(1) 2-n
(2)
(2)

(1)设等差数列{an}的公差为d,由已知条件可得
a1+d=0,2a1+12d=-10 a1=1,d=-1
a1=1,d=-1
故数列{an}的通项公式为an=2-n (2) 设数列{ }的前n项各为Sn,即Sn=a1+
}的前n项各为Sn,即Sn=a1+ +…+
+…+ ①
①

 =
= +
+ +…+
+…+ ②
②
所以,当 时,①-②得
时,①-②得
 = a1+
= a1+ +…+
+…+ -
-
=1-( +…+
+…+ )-
)-
=1-(1- )-
)- =
=
即Sn=
综上,数列数列{ }的前n项和Sn=
}的前n项和Sn=
a1+d=0,2a1+12d=-10
 a1=1,d=-1
a1=1,d=-1故数列{an}的通项公式为an=2-n (2) 设数列{
 }的前n项各为Sn,即Sn=a1+
}的前n项各为Sn,即Sn=a1+ +…+
+…+ ①
①
 =
= +
+ +…+
+…+ ②
②所以,当
 时,①-②得
时,①-②得 = a1+
= a1+ +…+
+…+ -
-
=1-(
 +…+
+…+ )-
)-
=1-(1-
 )-
)- =
=
即Sn=

综上,数列数列{
 }的前n项和Sn=
}的前n项和Sn=

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
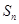 为等差数列
为等差数列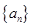 的前
的前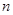 项和,已知
项和,已知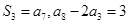 .
.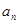 ;
;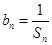 ,数列
,数列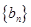 的前
的前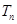 ,求证:
,求证: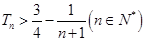 .
. 千元时多卖出
千元时多卖出 件。
件。 与n的函数关系式;
与n的函数关系式; 时,厂家应该生产多少件产品,做几千元的广告,才能获利最大?
时,厂家应该生产多少件产品,做几千元的广告,才能获利最大? ):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:
):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如: ;
; 为数表中第
为数表中第 行的第
行的第 个数.
个数. 和
和 ;
; 关于
关于 )的表达式;
)的表达式; ,
, ,试求一个等比数列
,试求一个等比数列 ,使得
,使得 ,且对于任意的
,且对于任意的 ,均存在实数
,均存在实数 ?,当
?,当 时,都有
时,都有 .
.
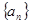 满足
满足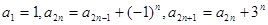 (
(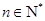 ).
).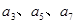 的值;
的值;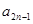 (用含
(用含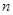 的式子表示);
的式子表示);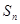 ,求
,求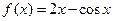 ,
,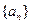 是公差为
是公差为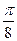 的等差数列,
的等差数列, ,则
,则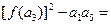 ( )
( )


 满足:对于
满足:对于 都有
都有 ,若
,若 ,则
,则 的通项公式为( )
的通项公式为( )



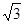 ,
,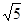 ,
,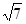 ,3,
,3,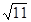 ,…,
,…,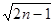 ,…,
,…,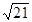 是这个数列的( )
是这个数列的( )