题目内容
已知p:关于x的不等式
(2t-1)dt-m>0对任意的x∈[1,2]恒成立;q:f(x)=
,且不等式f(m2)>f(m+2)恒成立,若p∨q为真,p∧q为假,求实数m的取值范围.
| ∫ | x 0 |
|
考点:复合命题的真假,定积分
专题:简易逻辑
分析:通过求定积分由p得,x2-x-m>0对任意的x∈[1,2]恒成立,从而能得到m<0;由函数f(x)解析式,能够判断该函数在R上为增函数,所以由q得,m2>m+2,解得m>2,或m<-1,而根据p∨q为真,p∧q为假得到p真q假,或p假q真两种情况,求出每种情况下m的取值范围再求并集即可.
解答:
解:由∫0x(2t-1)dt-m>0对任意x∈[1,2]恒成立;
得x2-x-m>0在x∈[1,2]上恒成立;
又函数y=x2-x-m=(x-
)2-
-m在[1,2]上是增函数;
∴其最小值为-m,因此只要-m>0即可,所以m<0;
即p:m<0;
因为y=x2在[0,+∞)上是增函数,∴y=x2≥0;
y=x-1在(-∞,0)上也是增函数,∴y=x-1<-1;
∴f(x)在R上是增函数,由f(m2)>f(m+2)可得m2>m+2;
解得m>2,或m<-1;
若p∨q为真,p∧q为假,则p,q一真一假;
∴
,或
;
∴-1≤m<0,或m>2;
∴实数m的取值范围为[-1,0)∪(2,+∞).
得x2-x-m>0在x∈[1,2]上恒成立;
又函数y=x2-x-m=(x-
| 1 |
| 2 |
| 1 |
| 4 |
∴其最小值为-m,因此只要-m>0即可,所以m<0;
即p:m<0;
因为y=x2在[0,+∞)上是增函数,∴y=x2≥0;
y=x-1在(-∞,0)上也是增函数,∴y=x-1<-1;
∴f(x)在R上是增函数,由f(m2)>f(m+2)可得m2>m+2;
解得m>2,或m<-1;
若p∨q为真,p∧q为假,则p,q一真一假;
∴
|
|
∴-1≤m<0,或m>2;
∴实数m的取值范围为[-1,0)∪(2,+∞).
点评:考查定积分的计算,二次函数的单调性,一次函数的单调性,以及分段函数单调性的判断方法,p∨q.p∧q真假和p,q真假的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
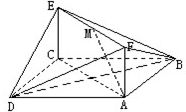 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= 抛物线有光学性质,从焦点出发的光经抛物线反射后沿平行于抛物线的对称轴方向射出,今有抛物线y2=2px(p>0),一光源在点A(6,4)处,由其发出的光线沿平行于抛物线的对称轴的方向射向抛物线上的B点,反射后,又射向抛物线上的C点,再反射后沿平行于抛物线的对称轴的方向射出,途中遇到直线l:x-y-7=0上的点D,再反射后又射回到A点,如图所示,则此抛物线的方程为( )
抛物线有光学性质,从焦点出发的光经抛物线反射后沿平行于抛物线的对称轴方向射出,今有抛物线y2=2px(p>0),一光源在点A(6,4)处,由其发出的光线沿平行于抛物线的对称轴的方向射向抛物线上的B点,反射后,又射向抛物线上的C点,再反射后沿平行于抛物线的对称轴的方向射出,途中遇到直线l:x-y-7=0上的点D,再反射后又射回到A点,如图所示,则此抛物线的方程为( )