题目内容
已知复数z=![]() -
-![]() i,w=
i,w=![]() +
+![]() i,复数
i,复数![]() ,z2w3在复平面上所对应的点分别为P、Q,
,z2w3在复平面上所对应的点分别为P、Q,
证明△OPQ是等腰直角三角形(其中O为原点).
证法一:由z=![]() -
-![]() i=cos(-
i=cos(-![]() )+isin(-
)+isin(-![]() ),
),
则z3=-i,又w=![]() +
+![]() i=cos
i=cos![]() +isin
+isin![]() ,
,
故w4=-1,于是![]() =
=![]() ·
·![]() =
=![]() =1
=1
由此可得OP⊥OQ,且|OP|=|OQ|,△OPQ有两边相等且其夹角为直角,故△OPQ为等腰直角三角形.
证法二:∵z=![]() -
-![]() i=cos(-
i=cos(-![]() )+isin(-
)+isin(-![]() )w=
)w=![]() +
+![]() i=cos
i=cos![]() +isin
+isin![]()
∴zw=cos![]() +isin
+isin![]()
![]() =cos(-
=cos(-![]() )+isin(-
)+isin(-![]() ),
),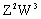 =cos(-
=cos(-![]() +
+![]() π)+isin(-
π)+isin(-![]() +
+![]() π)
π)
=cos![]() +isin
+isin![]() 。
。
因此,OP与OQ的夹角为![]() -(-
-(-![]() )=
)=![]()
所以OP⊥OQ
又|OP|=|![]() |=1,|OQ|=|z2w2|=1,所以|OP|=|OQ|,即得△OPQ是以点Q为直角顶点的等腰直角三角形.
|=1,|OQ|=|z2w2|=1,所以|OP|=|OQ|,即得△OPQ是以点Q为直角顶点的等腰直角三角形.
证法三:同证法一,得q3=-i. w4=-1,
∴|OP|=|z2w3|=|z2||w3|=1
|OQ|=|![]() |=|z|·|w|=1
|=|z|·|w|=1
|PQ|2=(z2w3-![]() )
)![]()
=(z2w3-![]() )(
)(![]() -zw)
-zw)
=2-z3w4-![]()
=2-i-(-i)
=2=|OP|2+|OQ|2
故△OPQ是以PQ为斜边的等腰直角三角形.
评述:本题综合考查复数的概念、运算、及其几何意义等基础知识,题目设计形式比较新颖,解题入口较宽,方法灵活,考查了考生基本的逻辑思维能力.

练习册系列答案
相关题目
 及|w|的值;
及|w|的值; 求实数a,b.
求实数a,b. 及|w|的值;
及|w|的值; 求实数a,b.
求实数a,b.