题目内容
8．若函数f（x）在x0处的导数f′（x0）=$\sqrt{3}$，则函数f（x）在x0处的切线的倾斜角为60°．分析 根据函数f（x）在x0处的导数f′（x0）与f（x）在x0处的切线斜率相等，利用斜率与倾斜角的关系求解即可．
解答 解：函数f（x）在x0处的导数f′（x0）与f（x）在x0处的切线斜率相等
∵f（x）在x0处的导数f′（x0）=$\sqrt{3}$，
∴函数f（x）在x0处的切线的斜率为$\sqrt{3}$，
函数f（x）在x0处的切线的倾斜角为60°
故答案为；60°
点评 本题考查了导数的概念，几何意义，准确理解概念即可，属于容易题．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
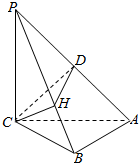在三棱锥P-ABC中，PC⊥平面ABC，△PAC是等腰直角三角形，PA=6，AB⊥BC，CH⊥PB，垂足为H，D为PA的中点，则当△CDH的面积最大时，CB=$\sqrt{6}$．
20．用二分法求方程x2=（$\frac{1}{2}$）x-2的近似解时，所取的初始区间可以是（ ）
| A． | （0，1） | B． | （1，2） | C． | （2，3） | D． | （3，4） |