题目内容
直线l经过点P(5,5),且和圆C:x2+y2=25相交,截得弦长为45,求l的方程.
直线l的方程为x-2y+5=0或2x-y-5=0.
如图所示,|OH|是圆心到直线l的距离,|OA|是圆的半径,|AH|是弦长|AB|的一半.在Rt△AHO中,|OA|=5,

 ,?
,?
∴ .
.
设直线l的方程为y-5=k(x-5).
∴ .
.
解得 或k=2.
或k=2.
∴直线l的方程为x-2y+5=0或2x-y-5=0.

 ,?
,?∴
 .
.设直线l的方程为y-5=k(x-5).
∴
 .
.解得
 或k=2.
或k=2.∴直线l的方程为x-2y+5=0或2x-y-5=0.

练习册系列答案
相关题目
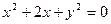 的圆心C,且与直线x+y=0垂直的直线方程是( )
的圆心C,且与直线x+y=0垂直的直线方程是( )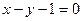
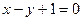
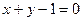
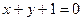
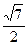 (O为原点),求直线l的方程。
(O为原点),求直线l的方程。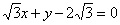 截圆x2+y2=4所得劣弧所对的圆心角为( )
截圆x2+y2=4所得劣弧所对的圆心角为( ) 
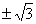
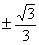
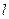 :
: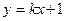 与圆C:
与圆C: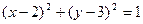 相交于
相交于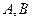 两点.
两点.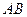 的中点
的中点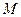 的轨迹方程;
的轨迹方程;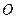 为坐标原点,
为坐标原点,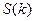 表示
表示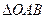 的面积,
的面积,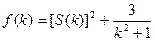 ,求
,求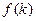 的最大值.
的最大值. 与圆
与圆 相交于两个不同点
相交于两个不同点 ,当
,当 取不同实数值时,求
取不同实数值时,求 中点的轨迹方程.
中点的轨迹方程.