Question

甲、乙两人各进行3次射击，甲每次击中目标的概率为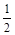，乙每次击中目标的概率为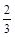

求：（1）乙至少击中目标2次的概率；

（2）乙恰好比甲多击中目标2次的概率

 

Answer 1

【答案】

（1）（2）

【解析】

试题分析：解： （1）乙至少击中目标2次的概率为

（2）设乙恰好比甲多击中目标2次为事件A，包含以下2个互斥事件

B₁：乙恰好击中目标2次且甲恰好击中目标0次

P（B₁）＝

B₂：乙恰好击中目标3次且甲恰好击中目标1次，

P（B₂）＝

则P（A）=P（B₁）+P（B₂）

所以，乙恰好比甲多击中目标2次的概率为

考点：独立重复试验

点评：独立重复试验的概率的求法：一般地，如果在一次试验中某事件发生的概率是P，那么在n次独立重复试验中这个事件恰好发生k次的概率。