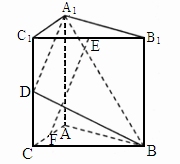
题目内容
如下图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.

(1)求证AE⊥平面BCE;
(2)求二面角B-AC-E的正弦值;
(3)求点D到平面ACE的距离.(只取前两问)
答案:
解析:
解析:
|
思路分析:(1)要证AE⊥平面BCE,需证明线线垂直.由条件易是:AE⊥BF,还需证AE垂直面内的另一直线,这就要考虑D-AB-E是直二面角,然后利用面面垂直的性质定理便可解决. (2)要求二面角B-AC-E的正弦,首先应构造出二面角的平面角,由(1)知AE⊥平面BCE,只要过B点作CE的垂线,便可利用线面垂直的判定定理构造平面角. 温馨提示:要熟练掌握线线、线面、面面垂直这三者之间的相互转化,尤其是面面垂直的性质要通过构造一个平面内交线的垂线才可利用面面垂直的性质定理转化为线面垂直. |

练习册系列答案
相关题目



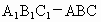 中,
中,
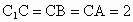
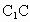 、
、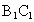 的中点.
的中点.
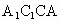 的距离;
的距离;
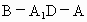 的大小;
的大小;
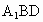 ?若存在,确定其位置并证明结论;若不存在,说明理由.
?若存在,确定其位置并证明结论;若不存在,说明理由.