题目内容
在△ABC中,已知tanA=
,tanB=
且最长边为
.
(Ⅰ)求∠C的值;
(Ⅱ)求△ABC最短边的长.
| 1 |
| 2 |
| 1 |
| 3 |
| 5 |
(Ⅰ)求∠C的值;
(Ⅱ)求△ABC最短边的长.
(Ⅰ)∵tanA=
,tanB=
,
∴tanC=-tan(A+B)=-
=-1,
又∵0<C<π,∴C=
;
(Ⅱ)易知最短边为AC,∵tanB=
,∠B为三角形内角,
∴cosB=
=
,sinB=
=
,
由正弦定理
=
,即
=
,
∴AC=1.
| 1 |
| 2 |
| 1 |
| 3 |
∴tanC=-tan(A+B)=-
| ||||
1-
|
又∵0<C<π,∴C=
| 3π |
| 4 |
(Ⅱ)易知最短边为AC,∵tanB=
| 1 |
| 3 |
∴cosB=
|
3
| ||
| 10 |
| 1-cos2B |
| ||
| 10 |
由正弦定理
| AC |
| sinB |
| AB |
| sinC |
| AC | ||||
|
| ||||
|
∴AC=1.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 的墙面前的点
的墙面前的点 处进行射击训练.已知点
处进行射击训练.已知点 ,某目标点
,某目标点 沿墙面的射击线
沿墙面的射击线 移动,此人为了准确瞄准目标点
移动,此人为了准确瞄准目标点 的大小.若
的大小.若 则
则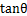 的最大值
的最大值 
 ,若
,若 ,则
,则 ( )
( )
