题目内容
如图是f（x）=Asin（ωx+θ）（|θ|＜| π | 2 |
分析：求A时根据最大值与最小值差的一半；求ω时，用周期；求θ时，用图象过点来求解．
解答：解：如图：A=
=1，
=
- (-
)=
∴T=π
由周期公式得ω=
=2
∴f（x）=sin（2x+θ）
又∵f（x）的图象过（-
，0）
∴sin(-
+θ) =0
又∵（|θ|＜
∴θ=
∴f(x)=sin(2x+
)
| 1-(-1) |
| 2 |
| T |
| 4 |
| π |
| 8 |
| π |
| 8 |
| π |
| 4 |
∴T=π
由周期公式得ω=
| 2π |
| T |
∴f（x）=sin（2x+θ）
又∵f（x）的图象过（-
| π |
| 8 |
∴sin(-
| π |
| 4 |
又∵（|θ|＜
| π |
| 2 |
∴θ=
| π |
| 4 |
∴f(x)=sin(2x+
| π |
| 4 |
点评：本题主要考查三角函数图象与解析式中各参数的内在联系，培养学生知图求式，以式知图的能力．
练习册系列答案
全能测控期末小状元系列答案
相关题目
如图是f（x）=x3+bx2+cx+d的图象，则x12+x22的值是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
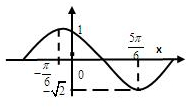F（x）=Asin的图象如图，f（x）=Asin（ωx+φ），（A＞0，0＜φ＜π）图象如图，则f（x）=
如图为f（x）=Asin（ωx+?）（A＞0，?＞0，?∈（-π，0））的图象的一段，
）的图象的一部分，则f（x）= 