题目内容
设 是函数
是函数 的导函数,
的导函数, 的图象如图所示,则
的图象如图所示,则 的图象最有可能的是( )
的图象最有可能的是( )
C
解析试题分析:根据给定的导函数图形可知,在x<0函数值为正,0<x<2时,函数值为负数,x>2为正数,说明了原函数先增后减再增,那么可以排除B,D,同时对于A,C来说,由于题目中给定了导函数与x轴 的交点为0,2,可知在这两个点处取得极值,因此排除A,选C.
考点:本试题考查了导函数的与函数的联系。
点评:根据导数的正负来确定原函数的单调增减性,同时利用导数的图像与坐标轴x轴的交点,说明了极值点问题,是解决试题的关键,属于中档题。

练习册系列答案
相关题目
已知函数 中,常数
中,常数 那么
那么 的解集为
的解集为
A.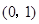 | B. | C. | D. |
已知函数 ,,则函数
,,则函数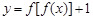 的零点个数是
的零点个数是
| A.4 | B.3 | C.2 | D.1 |
若a是函数 的零点,若
的零点,若 ,则
,则 的值满足
的值满足
A. | B. | C. | D. 的符号不确定 的符号不确定 |
函数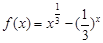 的零点个数为
的零点个数为
| A.0 | B.1 |
| C.2 | D.3 |
函数y= 的定义域为( )
的定义域为( )
A.(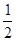 ,+∞) ,+∞) | B.[1,+∞ | C.( 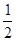 ,1 ,1 | D.(-∞,1)) |
函数 在区间
在区间 单调递增,则实数
单调递增,则实数 的取值范围为
的取值范围为
A. | B. | C. | D. |
若对任意的 ,函数
,函数 满足
满足 ,且
,且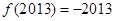 ,则
,则 ( )
( )
| A.0 | B.1 | C.-2013 | D.2013 |
 的图象的大致形状是
的图象的大致形状是 