题目内容
已知函数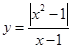 的图像与函数
的图像与函数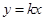 的图像恰有两个交点,则实数
的图像恰有两个交点,则实数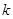 的取值范围是 .
的取值范围是 .
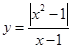 的图像与函数
的图像与函数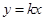 的图像恰有两个交点,则实数
的图像恰有两个交点,则实数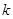 的取值范围是 .
的取值范围是 . .
.法一:数形结合图像法,函数 与函数
与函数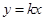 的恰好有两个交点,如图,因为
的恰好有两个交点,如图,因为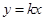 过定点
过定点
所以 或
或 故
故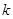 的范围为
的范围为 .
.

法二:直接法:函数
与函数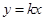 的恰好有两个交点,,①当
的恰好有两个交点,,①当
时,方程 得
得 在
在 与
与 单调递减,故
单调递减,故 ;②当
;②当 ,由
,由 ,
,
有
 ,解得,
,解得, 或
或 ,
,
则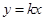 与
与 每一段函数有且只有一个交点,那么
每一段函数有且只有一个交点,那么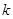 同时满足①②,故
同时满足①②,故
 .答案
.答案 .
.
【考点定位】本题考察了分段函数数与未知函数交点情况去求参数取值范围的问题,着重强调了分段函数要分段讨论,特别体现了形结合这种思想在解题中的巨大作用,考察了学生对函数图像、性质的把握,对函数的分段讨论的思想,需要较强的想象、推理能力
 与函数
与函数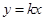 的恰好有两个交点,如图,因为
的恰好有两个交点,如图,因为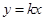 过定点
过定点
所以
 或
或 故
故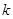 的范围为
的范围为 .
.
法二:直接法:函数

与函数
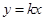 的恰好有两个交点,,①当
的恰好有两个交点,,①当
时,方程
 得
得 在
在 与
与 单调递减,故
单调递减,故 ;②当
;②当 ,由
,由 ,
,有

 ,解得,
,解得, 或
或 ,
,则
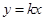 与
与 每一段函数有且只有一个交点,那么
每一段函数有且只有一个交点,那么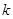 同时满足①②,故
同时满足①②,故
 .答案
.答案 .
.【考点定位】本题考察了分段函数数与未知函数交点情况去求参数取值范围的问题,着重强调了分段函数要分段讨论,特别体现了形结合这种思想在解题中的巨大作用,考察了学生对函数图像、性质的把握,对函数的分段讨论的思想,需要较强的想象、推理能力

练习册系列答案
相关题目
 和
和 构成的面积为200平方米的十字形地域。计划在正方形
构成的面积为200平方米的十字形地域。计划在正方形 上建一座花坛,造价每平方米4200元,并在四周的四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角上铺草坪,造价为每平方米80元。
上建一座花坛,造价每平方米4200元,并在四周的四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角上铺草坪,造价为每平方米80元。
 元,
元, 长为
长为 米,试求
米,试求 ,其中
,其中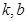 是常数,其图像是一条直线,称这个函数为线性函数,而对于非线性可导函数
是常数,其图像是一条直线,称这个函数为线性函数,而对于非线性可导函数 ,在已知点
,在已知点 附近一点
附近一点 的函数值
的函数值 ,利用这一方法,对于实数
,利用这一方法,对于实数 ,取
,取 在区间
在区间 内函数的导数为正,且
内函数的导数为正,且 ≤0,则函数
≤0,则函数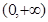 上为增函数的是( )
上为增函数的是( ) ;
; ;
; ;
; ;
;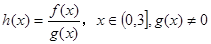 ,对任意
,对任意 恒成立,则( ).
恒成立,则( ).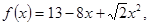 且
且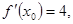 则
则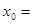
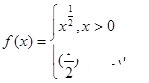 则
则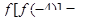




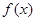 对于区间D内任意的
对于区间D内任意的 ,有
,有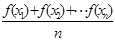
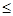
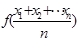 成立,称
成立,称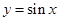 在区间
在区间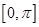 上是“凸函数”,则在△
上是“凸函数”,则在△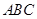 中,
中,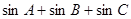 的最大值是( )
的最大值是( )


