题目内容
 如图所示的几何体中,四边形ABCD是等腰梯形,AD∥CD,∠DAB=60°
如图所示的几何体中,四边形ABCD是等腰梯形,AD∥CD,∠DAB=60°FC⊥平面ABCD,AE⊥BD,CB=CD=CF.
(1)求证:平面ABCD⊥平面AED;
(2)直线AF与面BDF所成角的余弦值.
考点:平面与平面垂直的判定,直线与平面所成的角
专题:空间位置关系与距离,空间角
分析:(1)由已知条件推导出AD⊥BD,又AE⊥BD,从而BD⊥平面AED,由此能证明平面ABCD⊥平面AED.
(2)连结AC,由CA,CB,CF两两垂直,以C为坐标原点,建立空间直角坐标系,利用向量法能求出直线AF与面BDF所成角的余弦值.
(2)连结AC,由CA,CB,CF两两垂直,以C为坐标原点,建立空间直角坐标系,利用向量法能求出直线AF与面BDF所成角的余弦值.
解答:
(1)证明:∵四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,
∴∠ADC=∠BCD=120°,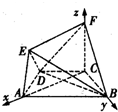
又CB=CD,∴∠CDB=30°,∴∠ADB=90°,AD⊥BD,
又AE⊥BD,且AE∩AD=A,AE,AD?平面AED,
∴BD⊥平面AED,∴平面ABCD⊥平面AED.
(2)解:连结AC,由(1)知AD⊥BD,∴AC⊥BC,
又FC⊥平面ABCD,∴CA,CB,CF两两垂直,
以C为坐标原点,建立空间直角坐标系,设CB=1,
则A(
,0,0),B(0,1,0),D(
,-
,0)
F(0,0,1),∴
=(
,-
,0),
=(0,-1,1),
(-
,0,1),
设平面BDF的一个法向量为
=(x,y,z),
则
,取z=1,得
=(
,1,1),
则cos<
,
>=-
∴cosθ=
.
∴直线AF与面BDF所成角的余弦值为
.…(12分)
∴∠ADC=∠BCD=120°,

又CB=CD,∴∠CDB=30°,∴∠ADB=90°,AD⊥BD,
又AE⊥BD,且AE∩AD=A,AE,AD?平面AED,
∴BD⊥平面AED,∴平面ABCD⊥平面AED.
(2)解:连结AC,由(1)知AD⊥BD,∴AC⊥BC,
又FC⊥平面ABCD,∴CA,CB,CF两两垂直,
以C为坐标原点,建立空间直角坐标系,设CB=1,
则A(
| 3 |
| ||
| 2 |
| 1 |
| 2 |
F(0,0,1),∴
| BD |
| ||
| 2 |
| 3 |
| 2 |
| BF |
| AF= |
| 3 |
设平面BDF的一个法向量为
| m |
则
|
| m |
| 3 |
则cos<
| AF |
| m |
| ||
| 5 |
∴cosθ=
2
| ||
| 5 |
∴直线AF与面BDF所成角的余弦值为
2
| ||
| 5 |
点评:本题考查平面与平面垂直的证明,考查直线与平面所成角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
已知样本点(xi,yi)(i=1,2,…,n)的散点图呈线性正相关,且回归直线的斜率估计值的绝对值为1.23,样本点的中心为(4,5),则回归直线方程为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
