题目内容
把偶函数y=f(x)的图象向右平移一个单位后得到的是一个奇函数的图象,则f(1)+f(2)+f(3)+…+f(9)的值为( )A.-9
B.0
C.9
D.-1
【答案】分析:由已知中偶函数y=f(x)的图象向右平移一个单位后得到的是一个奇函数的图象,我们可以得到函数的图象即是轴对称图形,又是中心对称图形,且对称轴和对称中心之间的距离为1,由此我们易得4为函数的一个周期,进而利用函数的周期性可以求出f(1)+f(2)+f(3)+…+f(9)的值.
解答:解:由已知函数y=f(x)为偶函数,
向右平移一个单位后,得到的是一个奇函数的图象可知,
f(-1)=0,且f(x-1)=-f(x+1),
即f(x+2)=-f(x),f(x+4)=f(x),
则函数是一个以4为周期的周期函数,
则f(1)+f(2)+f(3)+…+f(9)=f(1)=-f(-1)=0,
故选B.
点评:本题考查的知识点是函数奇偶性的性质,函数的周期性,其中根据函数奇偶性的性质,判断出函数的周期,进而化简f(1)+f(2)+f(3)+…+f(9)是解答本题的关键.
解答:解:由已知函数y=f(x)为偶函数,
向右平移一个单位后,得到的是一个奇函数的图象可知,
f(-1)=0,且f(x-1)=-f(x+1),
即f(x+2)=-f(x),f(x+4)=f(x),
则函数是一个以4为周期的周期函数,
则f(1)+f(2)+f(3)+…+f(9)=f(1)=-f(-1)=0,
故选B.
点评:本题考查的知识点是函数奇偶性的性质,函数的周期性,其中根据函数奇偶性的性质,判断出函数的周期,进而化简f(1)+f(2)+f(3)+…+f(9)是解答本题的关键.

练习册系列答案
相关题目
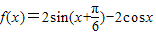 .
.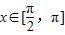 时,若
时,若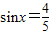 ,求函数f(x)的值;
,求函数f(x)的值; 时,求函数
时,求函数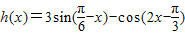 的值域;
的值域;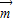 平移得到函数g(x)的图象,若函数g(x)是偶函数,写出
平移得到函数g(x)的图象,若函数g(x)是偶函数,写出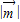 最小的向量
最小的向量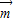 的坐标.
的坐标.