题目内容
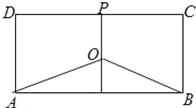
【题目】已知椭圆C的中心在原点O,焦点在x轴上,椭圆的两焦点与椭圆短轴的一个端点构成等边三角形,右焦点到右顶点的距离为1.
(1)求椭圆C的标准方程;
(2)是否存在与椭圆C交于A,B两点的直线l:![]() ,使得
,使得![]() 成立?若存在,求出实数m的取值范围;若不存在,请说明理由.
成立?若存在,求出实数m的取值范围;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在;实数m的取值范围是
;(2)存在;实数m的取值范围是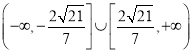
【解析】
(1)设椭圆的顶点为P,则![]() ,又由
,又由![]() ,由
,由![]() 结合椭圆的定义可得
结合椭圆的定义可得![]() ,结合
,结合![]() 可求椭圆的方程;
可求椭圆的方程;
(2)存在直线l,使得![]() 成立.设直线l的方程为
成立.设直线l的方程为![]() ,由
,由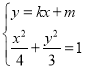 得
得![]() .由此利用根的判别式和韦达定理结合已知条件能求出实数m的取值范围.
.由此利用根的判别式和韦达定理结合已知条件能求出实数m的取值范围.
(1)设椭圆的顶点为P,
由两焦点与椭圆短轴的一个端点构成等边三角形,
可得![]() ,
,
又![]() 右焦点到右顶点的距离为1.
右焦点到右顶点的距离为1.
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
椭圆的方程为:![]() ;
;
(2)存在直线l,使得![]() 成立.理由如下:
成立.理由如下:
设直线l的方程为![]() ,
,
由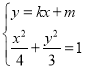 得
得![]() .
.
![]() ,化简得
,化简得![]() .
.
设![]() ,
,![]() ,则
,则
![]() ,
,![]() .
.
若![]() 成立,
成立,
即![]() ,等价于
,等价于![]() .
.
所以![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
化简得![]() .即
.即![]() ,
,
代入![]() 中,
中,![]() ,
,
解得![]() .
.
又由![]() ,得
,得![]() ,
,
从而![]() ,
,
解得![]() 或
或![]() .
.
所以实数m的取值范围是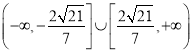 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目