题目内容
如图: 在 中,角
中,角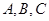 的对边分别为
的对边分别为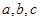

(Ⅰ) 若 边上的中点为
边上的中点为 ,且
,且 ,
,
求证: ;
;
(Ⅱ) 若 是锐角三角形,且
是锐角三角形,且 .
.
求 的取值范围.
的取值范围.
(Ⅰ) 在 中:
中: ,在
,在 中:
中:  ,
,


 (Ⅱ)
(Ⅱ) 
解析试题分析:(Ⅰ) 法1: 在 中:
中: ①
①
在 中:
中:  ②
②




法2:利用 推证更简捷.
推证更简捷.
(Ⅱ) 
 ,又
,又 为锐角三角形,
为锐角三角形,
故 .从而
.从而 .
.




 .
. ,
, .故
.故
考点:解三角形及三角函数化简求值
点评:解三角形常借助于正余弦定理,本题第一问中把握住有公共边的两三角形之间的联系得到m与三边关系式,第二问求三角函数值的范围都要将其化简为 的形式
的形式

练习册系列答案
相关题目
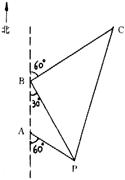
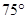 的方向上,距离为
的方向上,距离为 海里,在A处看灯塔C在货轮的北偏西
海里,在A处看灯塔C在货轮的北偏西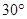 的方向上,距离为
的方向上,距离为 海里,货轮由A处向正北航行到D处时,再看灯塔B在南偏东
海里,货轮由A处向正北航行到D处时,再看灯塔B在南偏东 方向上,求:
方向上,求: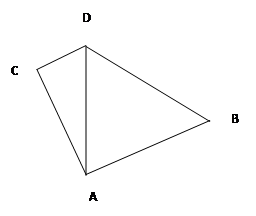

 的最大值为2.
的最大值为2.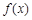 在
在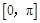 上的值域;
上的值域;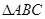 外接圆半径
外接圆半径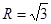 ,
,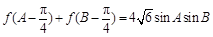 ,角A,B所对的边分别是a,b,求
,角A,B所对的边分别是a,b,求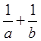 的值.
的值.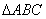 中,内角A,B,C的对边分别为
中,内角A,B,C的对边分别为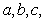 且
且 ,b=2,求A的值。
,b=2,求A的值。 中,
中,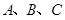 是三角形的三内角,
是三角形的三内角,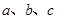 是三内角对应的三边,已知
是三内角对应的三边,已知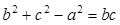 。
。 的大小;
的大小;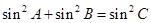 ,求角
,求角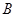 的大小。
的大小。 中,边
中,边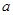 、
、 、
、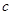 分别是角
分别是角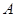 、
、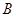 、
、 的对边,且满足
的对边,且满足 .
.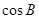 ;
;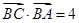 ,
,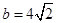 ,求边
,求边 中,角
中,角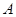 、
、 、
、 的对边分别为
的对边分别为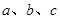 ,且满足
,且满足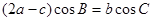 ,
, 、求角
、求角 、若
、若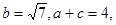 求
求 中,三个内角
中,三个内角 所对的边分别是
所对的边分别是
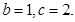
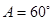 ,求
,求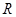
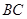 边上的中线长为
边上的中线长为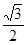 ,求
,求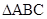 的面积。
的面积。