Question

12．设函数f（x）=$\frac{1}{3}$x³+bx²+cx+1（b、c∈R）存在极值点，且在区间（-∞，-1），（1，+∞）上均为单调增函数，则f（1）的取值范围是$[\frac{1}{3}，+∞）$．

Answer 1

分析 求出函数的导数，由单调递区间的端点可得不等式组，表示出f（1），利用线性规划求解表达式的范围．

解答 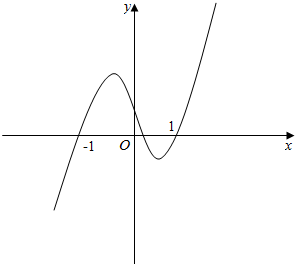解：函数f（x）=$\frac{1}{3}$x³+bx²+cx+1可得：f'（x）=x²+2bx+c，
依题意有$\left\{\begin{array}{l}f′（-1）＞0\\ f′（1）＞0\end{array}\right.$，即$\left\{\begin{array}{l}1-2b+c＞0\\ 1+2b+c＞0\end{array}\right.$，f（1）=$\frac{4}{3}+b+c$，

当f（1）=$\frac{4}{3}+b+c$经过A时，f（1）取得最小值，由$\left\{\begin{array}{l}1-2b+c=0\\ 1+2b+c=0\end{array}\right.$，可得A（-1，0），

f（1）的最小值为：$\frac{4}{3}+0-1$=$\frac{1}{3}$．
f（1）的取值范围是：[$\frac{1}{3}，+∞$）．

故答案为：$[\frac{1}{3}，+∞）$．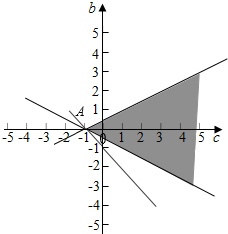

点评 本题考查利用导数研究函数的极值以及图象法，函数图象是表述函数问题的重要工具，因此，巧妙运用函数图象，能够变抽象思维为形象思维，利用线性规划，有助于把握数学问题的本质．