题目内容
13.已知命题p:“若直线x+ay+1=0与直线x-ay+2=0垂直,则a=1”;命题q:“a${\;}^{\frac{1}{3}}$>b${\;}^{\frac{1}{3}}$是a>b”的充要条件,则( )| A. | p真q假 | B. | p假q真 | C. | p且q为真 | D. | p或q为假 |
分析 根据条件先判断命题p,q的真假,然后根据复合命题之间的关系即可得到结论.
解答 解:由题意可知a≠0,若若直线x+ay+1=0与直线x-ay+2=0垂直,则-$\frac{1}{a}$×$\frac{1}{a}$=-1,解得a=±1,
∴p假,
由于y=${x}^{\frac{1}{3}}$ 为增函数,a${\;}^{\frac{1}{3}}$>b${\;}^{\frac{1}{3}}$⇒a>b,
由a>b⇒a${\;}^{\frac{1}{3}}$>b${\;}^{\frac{1}{3}}$,
∴“a${\;}^{\frac{1}{3}}$>b${\;}^{\frac{1}{3}}$是a>b”的充要条件,
∴q真,
故选:B.
点评 本题主要考查复合命题真假之间的关系,根据条件求出命题p,q的真假是解决本题的关键,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.设x,y满足约束条件$\left\{{\begin{array}{l}{x≥1}\\{x-2y≤0}\\{y-2≤0}\end{array}}\right.$,则z=x+2y-3的最大值为( )
| A. | 8 | B. | 5 | C. | 2 | D. | 1 |
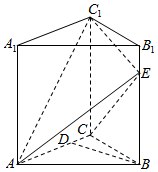 如图,直三棱柱ABC-A1B1C1中,AB=AC=AA1=4,BC=2$\sqrt{2}$,BD⊥AC,垂足为D,E为棱BB1上一点,BD∥平面AC1E.
如图,直三棱柱ABC-A1B1C1中,AB=AC=AA1=4,BC=2$\sqrt{2}$,BD⊥AC,垂足为D,E为棱BB1上一点,BD∥平面AC1E.