题目内容
某种家用电器每台的销售利润与该电器的无故障时间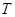 (单位:年)有关,若
(单位:年)有关,若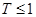 ,则销售利润为0元;若
,则销售利润为0元;若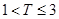 ,则销售利润为100元,若
,则销售利润为100元,若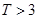 ,则销售利润为200元.设每台该种电器的无故障使用时间
,则销售利润为200元.设每台该种电器的无故障使用时间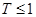 ,
,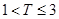 ,
,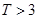 这三种情况发生的概率分别为
这三种情况发生的概率分别为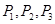 ,又知
,又知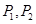 为方程
为方程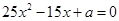 的两根,且
的两根,且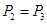 .
.
(1)求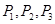 的值;
的值;
(2)记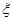 表示销售两台这种家用电器的销售利润总和,求
表示销售两台这种家用电器的销售利润总和,求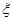 的分布列及数学期望.
的分布列及数学期望.
(Ⅰ) 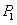 =
=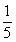 ,
,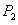 =
=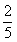 ,
,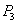 =
=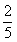 .
.
(Ⅱ)随机变量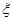 的分布列为
的分布列为
所求的数学期望为E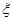
0 100 200 300 400 p 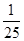
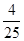
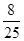
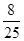
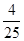
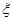 =0
=0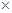
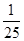 +100
+100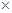
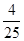 +200
+200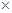
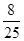 +300
+300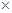
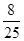 +400
+400
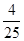 =240(元)
=240(元)
解析试题分析:(Ⅰ)由已知得 :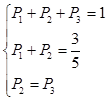
解得: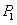 =
=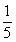 ,
,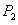 =
=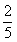 ,
,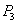 =
=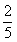 .
.
(Ⅱ)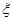 的可能取值为0,100,200,300,400.
的可能取值为0,100,200,300,400.
P(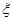 ="0)="
="0)=" 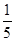
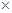
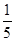 =
=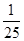 P(
P(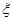 ="100)=" 2
="100)=" 2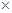
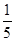
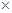
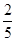 =
=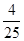
P(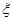 ="200)=" 2
="200)=" 2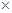
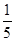
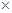
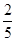 +
+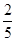
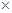
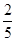 =
=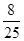 P(
P(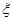 ="300)=" 2
="300)=" 2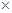
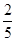
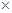
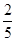 =
=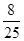
P(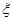 ="400)="
="400)=" 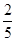
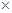
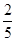 =
=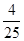
随机变量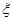 的分布列为
的分布列为
所求的数学期望为E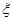
0 100 200 300 400 p 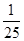
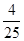
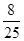
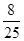
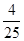

练习册系列答案
相关题目
某医院将一专家门诊已诊的1000例病人的病情及诊断所用时间(单位:分钟)进行了统计,如下表.若视频率为概率,请用有关知识解决下列问题.
| 病症及代号 | 普通病症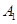 | 复诊病症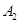 | 常见病症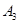 | 疑难病症 | 特殊病症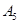 |
| 人数 | 100 | 300 | 200 | 300 | 100 |
| 每人就诊时间(单位:分钟) | 3 | 4 | 5 | 6 | 7 |
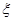 表示某病人诊断所需时间,求
表示某病人诊断所需时间,求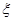 的数学期望.
的数学期望.并以此估计专家一上午(按3小时计算)可诊断多少病人;
某病人按序号排在第三号就诊,设他等待的时间为
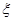 ,求
,求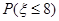 ;
;求专家诊断完三个病人恰好用了一刻钟的概率.
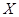 ,求
,求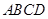 的边长为2,
的边长为2, 分别是边
分别是边 的中点.
的中点. ,求满足
,求满足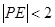 的概率;
的概率; 这八个点中,随机选取两个点,记这两个点之间的距离的平方为
这八个点中,随机选取两个点,记这两个点之间的距离的平方为 ,求
,求 .
. 表示所选用的两种不同的添加剂的芳香度之和。
表示所选用的两种不同的添加剂的芳香度之和。 。(要求写出计算过程或说明道理)
。(要求写出计算过程或说明道理) ,先从中任取三张卡片,将卡片上的数字相加,设数字和为
,先从中任取三张卡片,将卡片上的数字相加,设数字和为 ,当
,当 时,奖励奖金
时,奖励奖金 元;当
元;当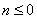 时,无奖励.
时,无奖励.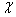 为奖金金额,求
为奖金金额,求 ,甲胜丙的概率为
,甲胜丙的概率为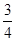 ,乙胜丙的概率为
,乙胜丙的概率为 。比赛顺序为:首先由甲和乙进行第一局的比赛,再由获胜者与未参加比赛的选手进行第二局的比赛,依此类推,在比赛中,有选手获胜满两局就取得比赛的胜利,比赛结束。
。比赛顺序为:首先由甲和乙进行第一局的比赛,再由获胜者与未参加比赛的选手进行第二局的比赛,依此类推,在比赛中,有选手获胜满两局就取得比赛的胜利,比赛结束。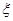 ,求
,求 。
。 元的奖金;若中两次奖,则共获得数额为
元的奖金;若中两次奖,则共获得数额为 元的奖金;若中3次奖,则共获得数额为
元的奖金;若中3次奖,则共获得数额为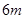 元的奖金。假设顾客每次抽奖中获的概率都是
元的奖金。假设顾客每次抽奖中获的概率都是 ,请问:商场将奖金数额m最高定为多少元,才能使促销方案对商场有利?
,请问:商场将奖金数额m最高定为多少元,才能使促销方案对商场有利?