题目内容
已知正方形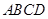 的边长为2,
的边长为2, 分别是边
分别是边 的中点.
的中点.
(1)在正方形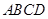 内部随机取一点
内部随机取一点 ,求满足
,求满足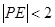 的概率;
的概率;
(2)从 这八个点中,随机选取两个点,记这两个点之间的距离的平方为
这八个点中,随机选取两个点,记这两个点之间的距离的平方为 ,求
,求 .
.
(1)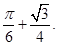
(2)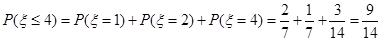
解析试题分析:解:(1)这是一个几何概型.所有点 构成的平面区域是正方形
构成的平面区域是正方形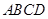 的内部,其面积是
的内部,其面积是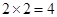 . 1分
. 1分
满足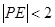 的点
的点 构成的平面区域是以
构成的平面区域是以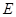 为圆心,2为半径的圆的内部与正方形
为圆心,2为半径的圆的内部与正方形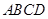 内部的公共部分,它可以看作是由一个以
内部的公共部分,它可以看作是由一个以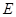 为圆心、2为半径、圆心角为
为圆心、2为半径、圆心角为 的扇形的内部与两个直角边分别为1和
的扇形的内部与两个直角边分别为1和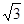 的直角三角形内部构成. 2分
的直角三角形内部构成. 2分
其面积是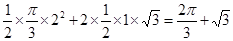 . 4分
. 4分
所以满足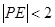 的概率为
的概率为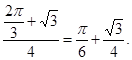 5分
5分
(2)从 这八个点中,任意选取两个点,共可构成
这八个点中,任意选取两个点,共可构成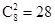 条不同的线段. 6分
条不同的线段. 6分
其中长度为1的线段有8条,长度为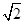 的线段有4条,长度为2的线段有6条,长度为
的线段有4条,长度为2的线段有6条,长度为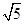 的线段有8条,长度为
的线段有8条,长度为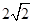 的线段有2条.所以
的线段有2条.所以 所有可能的取值为
所有可能的取值为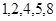 . 7分
. 7分
且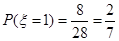 ,
, 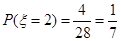 ,
, 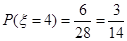
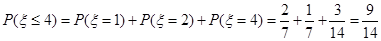 . 12分
. 12分
考点:古典概型的概率
点评:主要是考查了古典概型的概率的求解运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 , B小区已经收到邀请的人选择参加“幸福愿景”座谈会的概率是
, B小区已经收到邀请的人选择参加“幸福愿景”座谈会的概率是 .
. ,试求
,试求 人参加当天的闯关比赛,已知甲获奖的概率为
人参加当天的闯关比赛,已知甲获奖的概率为 ,乙获奖的概率为
,乙获奖的概率为 ,丙获奖而甲没有获奖的概率为
,丙获奖而甲没有获奖的概率为 。
。
 ,
, ,
, 的三个小球,现从这个盒子中,有放回地先后抽得两个小球的标号分别为
的三个小球,现从这个盒子中,有放回地先后抽得两个小球的标号分别为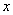 、
、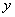 ,设
,设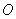 为坐标原点,设
为坐标原点,设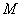 的坐标为
的坐标为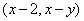 .
. 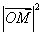 的所有取值之和;
的所有取值之和;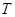 (单位:年)有关,若
(单位:年)有关,若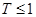 ,则销售利润为0元;若
,则销售利润为0元;若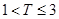 ,则销售利润为100元,若
,则销售利润为100元,若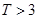 ,则销售利润为200元.设每台该种电器的无故障使用时间
,则销售利润为200元.设每台该种电器的无故障使用时间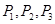 ,又知
,又知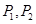 为方程
为方程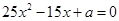 的两根,且
的两根,且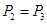 .
.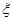 表示销售两台这种家用电器的销售利润总和,求
表示销售两台这种家用电器的销售利润总和,求 =
= (
( =1,2,3,4,5).
=1,2,3,4,5). 的值;
的值; ;
;