题目内容
已知{an}是首项为a1，公比为q（q≠1）的等比数列，其前n项和为Sn，且有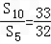
，设bn=2q+Sn．
（1）求q的值；
（2）数列{bn}能否为等比数列？若能，请求出a1的值；若不能，请说明理由．
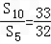，设bn=2q+Sn．（1）求q的值；
（2）数列{bn}能否为等比数列？若能，请求出a1的值；若不能，请说明理由．
解：（1）∵q≠1，
∴
=
=
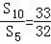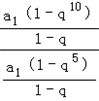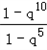=1+q5，
∴q=
．
（2）∵bn=2q+Sn =1+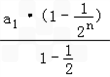
=（2a1+1）﹣
．
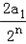若数列{bn}能为等比数列，则有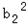
=b1 b3，
∴
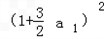=（1+a1 ）（1+
a1），
解得 a1=﹣
，或 a1=0 （舍去）．
∵bn≠0，且当n≥2时，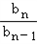
=
，
故当 a1=﹣
时，数列{bn}为等比数列．
∴
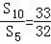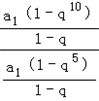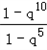===1+q5，∴q=
．（2）∵bn=2q+Sn =1+
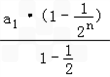=（2a1+1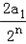）﹣．若数列{bn}能为等比数列，则有
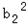=b1 b3，∴
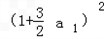=（1+a1 ）（1+a1），解得 a1=﹣
，或 a1=0 （舍去）．∵bn≠0，且当n≥2时，
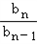=，故当 a1=﹣
时，数列{bn}为等比数列．
练习册系列答案
相关题目
已知{an}是首项为1的等比数列，Sn是{an}的前n项和，且9S3=S6，则数列{
}的前5项和为（ ）
| 1 |
| an |
A、
| ||
B、
| ||
C、
| ||
D、
|