题目内容
如图，E、F、G、H是矩形ABCD的四边中点，EF、AH交于点N，GH、FC交于点M，AD=8 cm，AB=6 cm,求四边形NFMH的面积.
思路分析：由于E、F、G、H都是中点，四边形NFMH应是平行四边形，并
FH等于矩形的长边.只要能求出△NFH和△FHM的公共边上的高,问题就解决了.
解：连结FH，过点M作QP⊥BC于P，交FH于Q.
∵FH BC，GC=
BC，
∴
=
=
=
.
∴PM=
QM.
又∵PQ=
CD=3 cm，
∴QM=
PQ=2 cm.
∴S四边形NFMH=2S△FMH
=2×
FH·QM
=2×
×8×2=16（cm2）.
练习册系列答案
阅读快车系列答案
相关题目
10、已知如图：E、F、G、H分别是正方体ABCD-A1B1C1D1的棱BC、CC1、C1D1、AA1的中点．
如图，E，F，G，H分别是正方体ABCD-A1B1C1D1的棱BC，CC1，C1D1，AA1的中点，求证：
如图，E、F、G、H分别是矩形ABCD的四条边的中点，向矩形ABCD所在的区域投针，则针尖在四边形EFGH内的概率为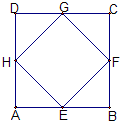
（2010•台州二模）如图，E，F，G，H分别是正方形ABCD各边的中点，将等腰 三角形EFB，FGC，GHD，HEA分别沿其底边折起，使其与原 所在平面成直二面角，则所形成的空间图形中，共有异面直线 段的对数为
如图，E、F、G、H分别是四边形ABCD的所在边的中点，若