题目内容
 如图,E,F,G,H分别是正方体ABCD-A1B1C1D1的棱BC,CC1,C1D1,AA1的中点,求证:
如图,E,F,G,H分别是正方体ABCD-A1B1C1D1的棱BC,CC1,C1D1,AA1的中点,求证:(1)GE∥平面BB1D1D;
(2)平面BDF∥平面B1D1H.
分析:(1)取B1D1的中点O,连接GO,OB,可证明四边形BEGO为平行四边形,利用线面平行的判定定理即可证得GE∥平面BB1D1D;
(2)由正方体的性质易知B1D1∥BD,取DD1中点P,连接AP,FP,可证BF∥D1H,再利用面面平行的判定定理即可.
(2)由正方体的性质易知B1D1∥BD,取DD1中点P,连接AP,FP,可证BF∥D1H,再利用面面平行的判定定理即可.
解答: 证明:
证明:
(1)如图,取B1D1的中点O,连接GO,OB,…(1分)
易证OG∥B1C1,
且OG=
B1C1,…(2分)
BE∥B1C1,
且BE=
B1C1…(3分)
∴OG∥BE且OG=BE,…(4分)
∴四边形BEGO为平行四边形,
∴OB∥GE…(5分)
∵OB?平面BDD1B1,GE?平面BDD1B1,
∴GE∥平面BB1D1D…(6分)
(2)由正方体的性质易知B1D1∥BD,
取DD1中点P,连接AP,FP,由于FP∥AB,且FP=AB,故四边ABFP为平行四边形,于是得AP∥FB,又HD1∥AP,故BF∥D1H,
∴BF∥D1H…(9分)
∵B1D1?平面BDF,BD?平面BDF,
∴B1D1∥平面BDF…(10分)
∵HD1?平面BDF,BF?平面BDF,
∴HD1∥平面BDF…(11分)
又∵B1D1∩HD1=D1,
∴平面BDF∥平面B1D1H…(12分)
 证明:
证明:(1)如图,取B1D1的中点O,连接GO,OB,…(1分)
易证OG∥B1C1,
且OG=
| 1 |
| 2 |
BE∥B1C1,
且BE=
| 1 |
| 2 |
∴OG∥BE且OG=BE,…(4分)
∴四边形BEGO为平行四边形,
∴OB∥GE…(5分)
∵OB?平面BDD1B1,GE?平面BDD1B1,
∴GE∥平面BB1D1D…(6分)
(2)由正方体的性质易知B1D1∥BD,
取DD1中点P,连接AP,FP,由于FP∥AB,且FP=AB,故四边ABFP为平行四边形,于是得AP∥FB,又HD1∥AP,故BF∥D1H,
∴BF∥D1H…(9分)
∵B1D1?平面BDF,BD?平面BDF,
∴B1D1∥平面BDF…(10分)
∵HD1?平面BDF,BF?平面BDF,
∴HD1∥平面BDF…(11分)
又∵B1D1∩HD1=D1,
∴平面BDF∥平面B1D1H…(12分)
点评:本题考查直线与平面的平行的判定与平面与平面平行的判定,合理的作出辅助线是证明的难点,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 10、已知如图:E、F、G、H分别是正方体ABCD-A1B1C1D1的棱BC、CC1、C1D1、AA1的中点.
10、已知如图:E、F、G、H分别是正方体ABCD-A1B1C1D1的棱BC、CC1、C1D1、AA1的中点. 如图,E、F、G、H分别是矩形ABCD的四条边的中点,向矩形ABCD所在的区域投针,则针尖在四边形EFGH内的概率为
如图,E、F、G、H分别是矩形ABCD的四条边的中点,向矩形ABCD所在的区域投针,则针尖在四边形EFGH内的概率为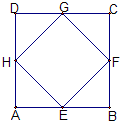 (2010•台州二模)如图,E,F,G,H分别是正方形ABCD各边的中点,将等腰 三角形EFB,FGC,GHD,HEA分别沿其底边折起,使其与原 所在平面成直二面角,则所形成的空间图形中,共有异面直线 段的对数为
(2010•台州二模)如图,E,F,G,H分别是正方形ABCD各边的中点,将等腰 三角形EFB,FGC,GHD,HEA分别沿其底边折起,使其与原 所在平面成直二面角,则所形成的空间图形中,共有异面直线 段的对数为 如图,E、F、G、H分别是四边形ABCD的所在边的中点,若
如图,E、F、G、H分别是四边形ABCD的所在边的中点,若