Question

【题目】已知函数有两个不同零点.设函数的定义域为,且的最大值记为,最小值记为．

（1）求（用表示）;

（2）当时,试问以为长度的线段能否构成一个三角形,如果不一定,进一步求出的取值范围,使它们能构成一个三角形;

（3）求和．

Answer 1

【答案】（1）（2）（3）．

【解析】

（1）因为为方程的两根,根据韦达定理可得: ，又，,即可得到答案;

（2）用求根公式求出得出 .根据三角形性质可得,只要 ,以为长度的线段就可以构成三角形;

（3）求出导函数,由已知可得时,,从而,函数在上单调递增,这样就可求出和.

（1） 为函数的两个零点，

为方程的两根，

由根与系数关系得:，又，

（2）当时,发现两根之和大于,两根之积小于,

两根一正一负,又 故

用来围成三角形的三条线段是,

,,与的大小关系无法判断，因此不一定能构成三角形，

又 若要构成三角形,则需两边之和大于第三边,且两边之差小于第三边，

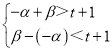即 ，即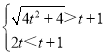，从而解得,

（3），

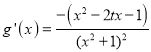是方程的两根，

由根与系数关系得:,

当时,,从而

函数在上单调递增，

．