题目内容
已知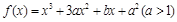 在
在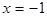 时有极值0。
时有极值0。
(1)求常数 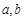 的值;
的值;
(2)求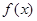 的单调区间。
的单调区间。
(3)方程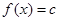 在区间[-4,0]上有三个不同的实根时实数
在区间[-4,0]上有三个不同的实根时实数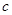 的范围。
的范围。
(1) (2)
(2)
解析试题分析:解:(1) ,由题知:
,由题知:
联立<1>、<2>有: (舍去)或
(舍去)或
(2)当 时,
时,
故方程 有根
有根 或
或
由表可见,当x 





+ 0 - 0 + 
↑ 极大值 ↓ 极小值 ↑  时,
时, 有极小值0,故
有极小值0,故 符合题意
符合题意
由上表可知: 的减函数区间为
的减函数区间为
 的增函数区间为
的增函数区间为 或
或
(3)因为 ,
,
由数形结合可得 。
。
考点:导数的运用
点评:解决的关键是根据导数判定函数单调性,进而确定函数的极值,属于基础题。

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间 上是减函数,又
上是减函数,又 .
. 的解析式;
的解析式; (m>0)上恒有
(m>0)上恒有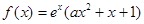 ,
,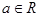 ;
; 的单调性;
的单调性; 上的最大值为
上的最大值为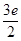 ,求
,求 的值.
的值. .(
.( )
) 时,试确定函数
时,试确定函数 在其定义域内的单调性;
在其定义域内的单调性; 上的最小值;
上的最小值; .
. 在区间
在区间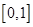 上是增函数,在区间
上是增函数,在区间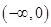 ,
,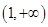 上是减函数,又
上是减函数,又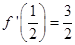
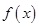 的解析式;
的解析式;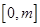
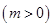 上恒有
上恒有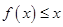 成立,求
成立,求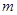 的取值范围
的取值范围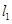 与直线4x-y-1=0平行,且点 P0 在第三象限,
与直线4x-y-1=0平行,且点 P0 在第三象限,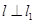 , 且 l 也过切点P0 ,求直线l的方程.
, 且 l 也过切点P0 ,求直线l的方程.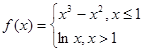 .
. 的单调递减区间;
的单调递减区间; 对一切
对一切 恒成立,求
恒成立,求 的取值范围.
的取值范围.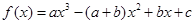 其中
其中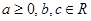
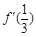 =0,求
=0,求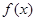 的单调区间;
的单调区间;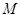 表示
表示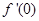 与
与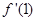 两个数中的最大值,求证:当0≤x≤1时,|
两个数中的最大值,求证:当0≤x≤1时,|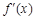 |≤
|≤ .
. 的单调区间与极值;
的单调区间与极值; ,使得对任意的
,使得对任意的 ,当
,当 时恒有
时恒有 成立.若存在,求
成立.若存在,求