Question

【题目】已知数列{an}的前n项和Sn ， 且Sn=2n2+3n；
（1）求它的通项an ．
（2）若bn= ，求数列{bn}的前n项和Tn ．

Answer 1

【答案】
（1）解：由Sn=2n2+3n，

当n=1时，a1=S1=5；

当n＞1时，an=Sn﹣Sn﹣1=2n2+3n﹣2（n﹣1）2﹣3（n﹣1）

=4n+1，对n=1也成立．

则通项an=4n+1；

（2）解：bn= = = （ ﹣ ），

即有前n项和Tn= （ ﹣ + ﹣ +…+ ﹣ ）

= （ ﹣ ）= ．

【解析】（1）由数列的通项和求和的关系：当n=1时，a1=S1 ， 当n＞1时，an=Sn﹣Sn﹣1 ， 化简即可得到所求通项；（2）求得bn= = = （ ﹣ ），再由数列的求和方法：裂项相消求和，化简整理即可得到所求和．
【考点精析】通过灵活运用数列的前n项和和等差数列的性质，掌握数列{an}的前n项和sn与通项an的关系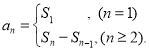；在等差数列{an}中，从第2项起，每一项是它相邻二项的等差中项；相隔等距离的项组成的数列是等差数列即可以解答此题．