题目内容
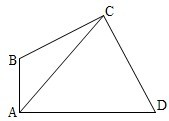 四边形ABCD中,
四边形ABCD中,. |
| AB |
. |
| BC |
. |
| CD |
. |
| DA |
. |
| AC |
分析:设所求向量的模为x,角B=θ,由∠DAB=∠BCD=90°,根据四边形的内角和表示出角D=π-θ,在三角形ABC中,利用余弦定理表示出cosθ,同理在三角形ACD中,利用余弦定理表示出cos(π-θ),根据诱导公式得到cosθ=-cos(π-θ),列出关于x的方程,求出方程的解即可得到x的值,进而所求向量的模.
解答:解:设|
=x,∠B=θ,
由∠DAB=∠BCD=90°,则∠D=180°-θ,
△ABC中,|
=1,|
|=5,|
=x,
则cosθ=
=
;
△ACD中,|
=5,|
=7,|
=x,
则cos(180°-θ)=
=
;
∵cos(180°-θ)=-cosθ,
∴
=-
?x=
=4
.
故答案为:4
. |
| AC| |
由∠DAB=∠BCD=90°,则∠D=180°-θ,
△ABC中,|
. |
| AB| |
. |
| BC |
. |
| AC| |
则cosθ=
| 12+52-x2 |
| 2×1×5 |
| 26-x2 |
| 10 |
△ACD中,|
. |
| CD| |
. |
| DA| |
. |
| AC| |
则cos(180°-θ)=
| 72+52-x2 |
| 2×7×5 |
| 74-x2 |
| 70 |
∵cos(180°-θ)=-cosθ,
∴
| 74-x2 |
| 70 |
| 26-x2 |
| 10 |
| 32 |
| 2 |
故答案为:4
| 2 |
点评:此题考查了余弦定理,以及四边形的内角和,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目
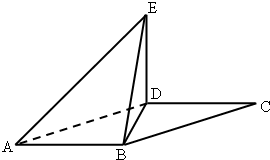 如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4将△CBD沿BD折起到△EBD的位置,使平面EDB⊥平面ABD.
如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4将△CBD沿BD折起到△EBD的位置,使平面EDB⊥平面ABD. (1)已知0<α<
(1)已知0<α<