题目内容
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,数列
,数列![]() 是公差为0的等差数列,且满足
是公差为0的等差数列,且满足![]() ,
,![]() 是
是![]() 和
和![]() 的等比数列.
的等比数列.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)求![]() ;
;
(3)设数列![]() 的通项公式
的通项公式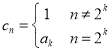
![]() ,求
,求![]() ;
;
【答案】(1)![]() ,
,![]() .(2)
.(2)![]() .(3)
.(3)![]() .
.
【解析】
(1)利用两式![]() (
(![]() ),
), ![]() (
(![]() )相减得到
)相减得到![]() (
(![]() ),再根据等比数列的通项公式可得
),再根据等比数列的通项公式可得![]() ,根据
,根据![]() 求得等差数列
求得等差数列![]() 的公差,再根据等差数列的通项公式可得
的公差,再根据等差数列的通项公式可得![]() ;
;
(2)根据![]() 裂项求和可得结果;
裂项求和可得结果;
(3)由![]() 的通项公式分析可知,数列
的通项公式分析可知,数列![]() 的前
的前![]() 项中,有
项中,有![]() 项的值不为1,它们是
项的值不为1,它们是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其余的项的值都为1,由此可得
,其余的项的值都为1,由此可得![]() ,然后利用等比数列的前
,然后利用等比数列的前![]() 项和公式可得结果.
项和公式可得结果.
(1)因为![]() (
(![]() ),所以
),所以![]() (
(![]() ),
),
两式相减,整理得:![]()
![]() ,
,
又当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() (
(![]() ),
),
所以![]() 是以6为首项,3为公比的等比数列,
是以6为首项,3为公比的等比数列,
![]() .
.
设等差数列![]() 的公差为
的公差为![]() ,
,
因为![]() ,
,![]() 是
是![]() 和
和![]() 的等比中项,
的等比中项,
所以![]() ,即
,即![]() ,
,
整理得![]() ,
,
解得![]() 或
或![]() ,因为公差不为0,
,因为公差不为0,
所以![]() ,
,
故![]() .
.
(2)因为![]() ,
,
所以![]() .
.
(3)因为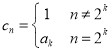
![]() ,
,![]() ,
,
所以数列![]() 的前
的前![]() 项中,有
项中,有![]() 项的值不为1,它们是
项的值不为1,它们是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其余的项的值都为1,
,其余的项的值都为1,
所以![]()
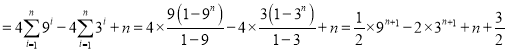 .
.

练习册系列答案
相关题目
【题目】随着我国经济结构调整和方式转变,社会对高质量人才的需求越来越大,因此考研现象在我国不断升温.某大学一学院甲、乙两个本科专业,研究生的报考和录取情况如下表,则
性别 | 甲专业报考人数 | 乙专业报考人数 | 性别 | 甲专业录取率 | 乙专业录取率 | |
男 | 100 | 400 | 男 |
|
| |
女 | 300 | 100 | 女 |
|
|
A.甲专业比乙专业的录取率高B.乙专业比甲专业的录取率高
C.男生比女生的录取率高D.女生比男生的录取率高